پردازش تصویر شامل طیف وسیعی از تکنیک ها و الگوریتم ها است که فرآیند های اصلی و پایه این تکنیک ها عبارتند از : تیز کردن ، حذف نویز ، رفع ماتی ، تشخیص لبه ، باینری کردن ، افزایش کنتراست ، و ناحیه بندی و برچسب گذاری اشیاء.
فهرست مطالب
تکنیک های مهم پردازش تصویر
تیز کردن ( sharpening ) باعث افزایش وضوح لبه ها و جزئیات دقیق یک تصویر ، جهت مشاهده بهتر توسط انسان می شود. این کار کنتراست یا تباین بین مناطق روشن و تاریک را برای نشان دادن ویژگی های تصویر افزایش می دهد. به طور کلی ، وضوح یا تیزکردن تصویر شامل اعمال فیلتر بالا گذر بر روی تصویر است.
در پردازش تصویر و تفسیر تصویر لازم است تا اطلاعات مفیدی بدست آوریم و تکنیک های حذف نویز ( noise removal ) ، میزان نویز موجود در تصویر را پیش از هر نوع پردازشی کاهش می دهد. تصاویر معمولا هم از دوربین های دیجیتال و هم از دوربین های فیلمبرداری معمولی ، از طریق منابع مختلف حاوی نویز می شوند. این منابع نویز شامل نویز فلفل نمکی ( نقاط تاریک و روشن پراکنده ) و نویز گوسی (مقادیر کاهش یافته پیکسل های تصویر) هستند. در هر صورت ، نویز در پیکسل های مختلف می تواند همبسته یا ناهمبسته باشد. در بسیاری از موارد ، مقادیر نویز در پیکسل های مختلف به صورت مستقل و یکسان توزیع شده و در نتیجه ناهمبسته هستند. در انتخاب الگوریتم کاهش نویز ، باید قدرت و سرعت رایانه موجود را در نظر گرفت و اینکه آیا از دست دادن جزئیات تصویر در صورت حذف نویز بیشتر ، قابل قبول است یا خیر.
رفع ماتی ( Deblurring ) فرآیند حذف اثرات مات شدگی از قبیل ماتی ناشی از متمرکز نبودن لنز یا ماتی حرکتی تصاویر است. مات شدگی به طور معمول به صورت کانولوشن یک تابع نقطه گستر ( point-spread function ) با یک تصویر ورودی واضح فرضی مدل می شود ، که هم تصویر ورودی واضح (که باید بازیابی شود) و هم تابع نقطه گستر ، ناشناخته است. الگوریتم های رفع ماتی شامل روش هایی برای حذف تاری از تصویر است. رفع ماتی یک فرایند تکرار شونده است و ممکن است لازم باشد یک روند را چندین بار تکرار کند تا تصویر نهایی بهترین تقریب از تصویر اصلی باشد.
استخراج لبه ( edge extraction ) یا تشخیص لبه های تصویر ، قبل از شناسایی محتویات آن و به منظور تفکیک اجسام از یکدیگر استفاده می شود. این تکنیک شامل انواع روش های ریاضی است که هدف آن ها شناسایی نقاطی از یک تصویر دیجیتالی است که در آن ها روشنایی تصویر به شدت تغییر می کند.
رویکردهای تشخیص لبه را می توان به دو روش مبتنی بر جستجو و رویکرد مبتنی بر عبور صفر تقسیم بندی کرد. روش های مبتنی بر جستجو ، ابتدا با محاسبه میزان قدرت لبه ( معمولاً یک تابع مشتق مرتبه اول ) مانند اندازه گرادیان و سپس جستجوی محلی حداکثر جهت دار در اندازه گرادیان ، با استفاده از یک تخمین جهت یابی محلی لبه (معمولا جهت گرادیان)، لبه ها را تشخیص می دهد. معمولاً روش های عبور صفر برای یافتن لبه ، به دنبال عبور صفر در یک تابع مشتق مرتبه دوم محاسبه شده از تصویر هستند. آشکارسازهای لبه مرتبه اول شامل آشکارساز لبه Canny ، عملگر های Prewitt و Sobel و غیره است.
رویکردهای دیگر شامل روش مشتق گیری مرتبه دوم برای تشخیص عبور صفر ، روش های همخوانی فازی (یا همدوسی فاز) یا Phase stretch transform (PST) است. روش مشتق مرتبه دوم عبور صفر ، دیفرانسیل مرتبه دوم در جهت گرادیان را تشخیص می دهد. روش های همدوسی فاز سعی می کند مکان هایی را در یک تصویر پیدا کند که در آن همه Sinusoid های حوزه فرکانس همفاز باشند. PST با شبیه سازی انتشار از طریق یک محیط پراش با ویژگی پراکندگی سه بعدی مهندسی شده (ضریب شکست) ، تصویر را تغییر می دهد.
باینری کردن تصویر ( binarisation ) به تبدیل تصویر مقیاس خاکستری به دو سطح خاکستری سیاه و سفید اشاره دارد. Thresholding یا آستانه گذاری یک تکنیک رایج برای تبدیل هر تصویر مقیاس خاکستری به یک تصویر باینری است.
افزایش کنتراست ( contrast enhancement ) جهت بهبود تصویر به منظور مشاهده بهتر انسان و همچنین عملیات پردازش تصویر انجام می شود. با استفاده بهینه از رنگ های موجود در صفحه نمایش یا دستگاه خروجی ، ویژگی های تصویر به وضوح متمایز می شود. دستکاری کنتراست شامل تغییر دامنه مقادیر کنتراست در یک تصویر است.
ناحیه بندی ( segmentation ) و برچسب گذاری ( labeling ) اشیاء در یک صحنه ، پیش نیاز بسیاری از سیستم های تشخیص و طبقه بندی اشیاء است. ناحیه بندی فرآیند اختصاص هر پیکسل در تصویر مرجع به دو یا چند کلاس است. ناحیه بندی تصویر فرآیند تقسیم تصویر دیجیتال به چند بخش (مجموعه ای از پیکسل ها ، که به عنوان super pixel نیز شناخته می شوند) است. هدف این است که نمایش کنتراست یک تصویر را بهبود دهیم و تصویر بدست آمده معنادارتر و تجزیه و تحلیل آن آسان تر باشد. پس از ناحیه بندی و برچسب گذاری اشیاء مربوطه ، می توان ویژگی های مربوطه آن ها را استخراج و برای طبقه بندی ، مقایسه ، خوشه بندی یا تشخیص اشیاء مورد نظر استفاده کرد.
انواع تصاویر
جعبه ابزار MATLAB از چهار نوع تصویر یعنی تصاویر مقیاس خاکستری ، تصاویر باینری ، تصاویر شاخص گذاری شده و تصاویر RGB پشتیبانی می کند. شرح مختصری از این نوع تصاویر در زیر آورده شده است.
تصاویر مقیاس خاکستری
این تصاویر به عنوان تصاویر تک رنگ نیز شناخته می شوند و شامل ۸ بیت در هر پیکسل هستند، که مقدار پیکسل ۰ مربوط به رنگ “سیاه” است ، مقدار پیکسل ۲۵۵ مربوط به رنگ “سفید” و مقادیر میانی نشان دهنده رنگ های مختلف خاکستری است که به صورت یک آرایه دو بعدی از پیکسل ها کدگذاری می شوند و هر پیکسل دارای ۸ بیت است.
تصاویر دودویی ( باینری )
این تصاویر از ۱ بیت در پیکسل استفاده می کنند ، که معمولاً مقدار ۰ به معنای رنگ “سیاه” و مقدار ۱ به معنی رنگ “سفید” است. این تصاویر به صورت یک آرایه دوبعدی نمایش داده می شوند. مزیت اصلی تصاویر باینری اندازه کوچک آن ها است.
تصاویر شاخص گذاری شده
این تصاویر ، ماتریسی از اعداد صحیح (X) هستند، که هر عدد صحیح به ردیف خاصی از مقادیر RGB در یک ماتریس ثانویه (نقشه) معروف به نقشه رنگی اشاره دارد.
تصویر رنگی RGB
در یک تصویر RGB ، هر پیکسل رنگی به صورت سه گانه حاوی مقادیر اجزای رنگی R ، G و B خود نشان داده شده است. در MATLAB ، یک تصویر رنگی RGB مربوط به یک آرایه سه بعدی با ابعاد M × N × ۳ است. که M و N به ترتیب طول و عرض تصویر هستند و ۳ تعداد اجزای رنگ است. برای تصاویر RGB کلاس دو ، محدوده مقادیر [۰٫۱] و برای کلاس های uint8 و uint16 ، محدوده به ترتیب [۰ ، ۲۵۵] و [۰ ، ۶۵۵۳۵] است.
اکثر الگوریتم های پردازش تصاویر تک رنگ با استفاده از تصاویر باینری یا مقیاس خاکستری انجام می شود.
کیفیت تصویر
کیفیت تصویر بر حسب رزولوشن یا وضوح مکانی و کمی سازی تعریف می شود. رزولوشن یا وضوح مکانی ، تراکم پیکسل بر روی تصویر است. هرچه وضوح مکانی بیشتر باشد ، پیکسل های بیشتری برای نمایش تصویر استفاده می شود. وضوح مکانی از نظر کیفی به صورت نقطه در اینچ (dpi) بیان می شود.
وضوح تصویر را می توان با استفاده از تابع imresize تغییر داد. دستور imresize (x,0.5)، اندازه تصویر را نصف می کند. این کار روی ماتریسی انجام می شود که دارای عناصری است که تعداد سطر و ستون آن زوج است. اما دستور imresize (x,2)، به این صورت عمل می کند که همه پیکسل ها تکرار می شوند تا تصویری با اندازه اصلی ، اما با نصف وضوح قبلی در هر جهت تولید شود.
سایر تغییرات وضوح را می توان با استفاده از فاکتور های مقیاس بندی مورد نظر انجام داد، برای مثال دستور imresize(imresize(x,1/2),2) وضوح تصویر را به نصف کاهش می دهد در حالی که اندازه تصویر را ثابت نگه می دارد. به طور مشابه ، دستور imresize(imresize(x,1/4),4) وضوح تصویر را یک چهارم تغییر می دهد. مجموعه دستورات زیر وضوح تصویر “Penguins_grey.jpg” را به نصف کاهش می دهد:
A = imread(‘Penguins_grey.jpg’); A1 = imresize((imresize(A,1/2)),2); imshow(A1)
شکل ۱ تصویر A1 را نشان می دهد.

A = imread(‘Penguins_grey.jpg’); A2 = imresize((imresize(A,1/4)),4); imshow(A2)
شکل ۲ تصویر A2 را نشان می دهد.

A = imread(‘Penguins_grey.jpg’); A3 = imresize((imresize(A,1/8)),8); imshow(A3)
شکل ۳ تصویر A3 را نشان می دهد.

کمی سازی تصویر را می توان به عنوان یک فرآیند نگاشت توصیف کرد که در آن گروهی از نقاط داده (چندین پیکسل در یک محدوده مقادیر خاکستری) در یک نقطه واحد (یک سطح خاکستری) ترسیم می شوند. با استفاده از تابع grayslice می توان یک تصویر را در MATLAB مجددا کمی سازی کرد. مجموعه دستورات زیر سطوح کمی سازی را به ۶۴ کاهش می دهد و تصویر را نمایش می دهد:
A = imread(‘Penguins_grey.jpg’); B=grayslice(A,64); imshow(B,gray(64))
تصویر حاصل از تابع imshow در شکل ۴ نشان داده شده است.

مجموعه دستورات زیر سطوح کمی سازی را به ۸ کاهش می دهد و تصویر را نمایش می دهد:
A = imread(‘Penguins_grey.jpg’); B=grayslice(A,8); imshow(B,gray(8))
تصویر حاصل از تابع imshow در شکل ۵ نشان داده شده است.

هیستوگرام
هیستوگرام یک تصویر در مقیاس خاکستری نشان دهنده فراوانی سطوح خاکستری آن است. در واقع هیستوگرام یک نمودار است که تعداد دفعات تکرار هر سطح خاکستری در تصویر را نشان می دهد. در یک تصویر تیره ، سطوح خاکستری (و از همچنین هیستوگرام) در انتهای پایینی تراکم بیشتری دارند. در یک تصویر یکنواخت روشن ، سطوح خاکستری (و در نتیجه هیستوگرام) در انتهای بالایی تراکم بیشتری دارند. در یک تصویر با کنتراست مطلوب ، سطوح خاکستری (و در نتیجه هیستوگرام) به خوبی در بیشتر محدوده های خاکستری پخش شده است.
در MATLAB ، هیستوگرام را می توان با استفاده از تابع imhist مشاهده کرد. به عنوان مثال ، دستورات زیر را می توان برای نمایش هیستوگرام تصویر Penguins_grey.jpg استفاده کرد:
A = imread(‘Penguins_grey.jpg’); figure(1), imhist(A);
شکل ۶ هیستوگرام تولید شده توسط دستور بالا را نشان می دهد.
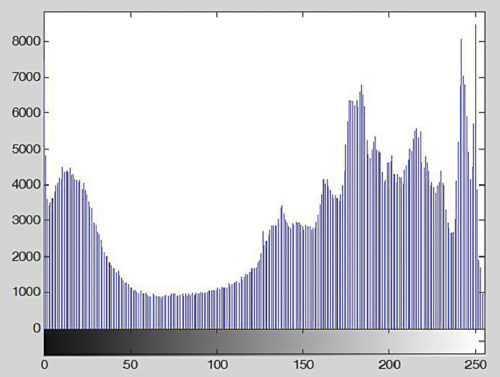
سه عملیات اصلی انجام شده بر روی هیستوگرام شامل گسترش هیستوگرام ، فشرده سازی هیستوگرام و لغزش هیستوگرام است. که در ادامه به توضیح این عملیات می پردازیم.
گسترش هیستوگرام
گسترش هیستوگرام یا ( histogram stretching ) ، که به عنوان برش ورودی نیز شناخته می شود ، شامل یک تغییر خطی است که بخشی از هیستوگرام اصلی را گسترش می دهد به طوری که محدوده روشنایی غیر صفر آن شامل مقیاس های خاکستری بیشتری باشد.
اگر هیستوگرام تصویر در مرکز تجمع بیشتری داشته باشد ، می توان با استفاده از تابع imadjust آن را کشیده تر کرد و بسط داد. دستور زیر هیستوگرام را مانند شکل ۷ بسط می دهد:
imadjust (F, [a,b], [c,d])
مقادیر a ، b ، c و d باید بین ۰ تا ۱ باشد.
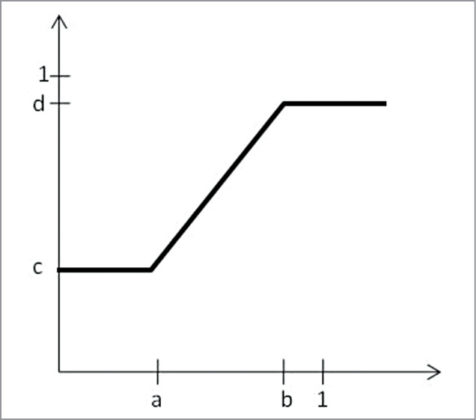
دستور imadjust (F, [], [1,0]) مقدار خاکستری تصویر را معکوس می کند و نتیجه ای مشابه نگاتیو عکاسی ایجاد می کند.
گسترش هیستوگرام با استفاده از دستورات بالا به ورودی کاربر نیاز دارد. یک روش جایگزین استفاده از دستور برابری هیستوگرام ( histogram equalisation ) است که یک روش کاملاً خودکار است. دستور برابری هیستوگرام در متلب histeq است. استفاده از دستور histeq در زیر نشان داده شده است:
A = imread(‘Penguins_grey.jpg’); HE = histeq(A); imshow(HE),figure, imhist(HE)
شکل ۸ و ۹ به ترتیب تصویر و برابری هیستوگرام آن را نشان می دهد.

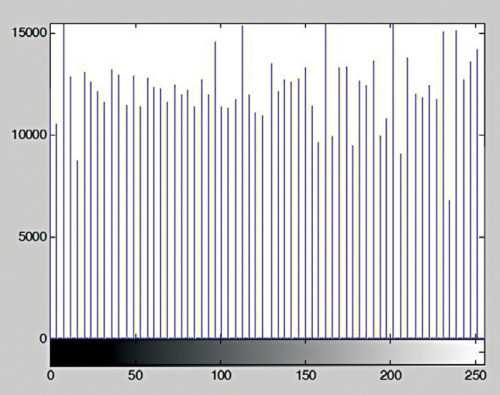
فشرده سازی هیستوگرام
فشرده سازی هیستوگرام یا ( histogram shrinking ) ، که به عنوان برش خروجی نیز شناخته می شود ، هیستوگرام اصلی را به گونه ای تغییر می دهد که محدوده مقیاس خاکستری آن در مقیاس خاکستری باریک تری فشرده شود. از تابع imadjust می توان برای کوچک کردن هیستوگرام استفاده کرد.
لغزش هیستوگرام
لغزش هیستوگرام یا ( histogram sliding ) شامل تفریق یا اضافه کردن یک مقدار روشنایی ثابت به تمام پیکسل های تصویر است. تاثیر کلی یک تصویر با ویژگی های کنتراست قابل مقایسه است ، اما به ترتیب روشنایی متوسط یا بالاتر. از توابع imadd و imsubtract می توان برای لغزش هیستوگرام استفاده کرد.
هنگام پیاده سازی این تکنیک ، باید مطمئن شوید که مقادیر پیکسل از محدوده مقیاس خاکستری خارج نمی شود. نمونه ای از لغزش هیستوگرام در زیر آورده شده است:
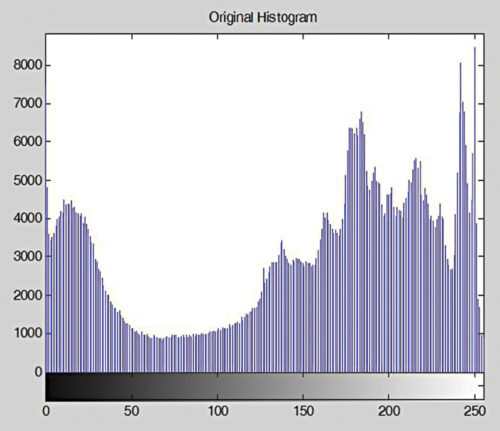
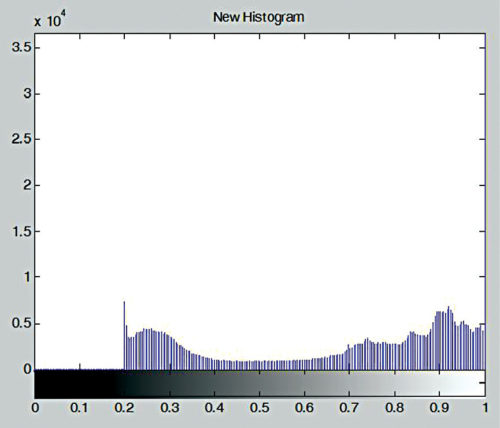
A = imread(‘Penguins_grey.jpg’); imshow(A),title(‘Original Image’); B=im2double(A); bright_add = 0.2; imhist(A), title(‘Original Histogram’); C=B+bright_add; imshow(C),title(‘New Bright Image’); imhist(C), title(‘New Histogram’);
در این مثال ، با افزودن مقدار ثابت ۰٫۲ به مقادیر پیکسل های تصویر ، نتیجه روشن تر خواهیم داشت. شکل ۱۰ و ۱۱ به ترتیب تصویر اصلی و هیستوگرام آن را نشان می دهد. و همچنین شکل ۱۲ و ۱۳ به ترتیب تصویر اصلاح شده و هیستوگرام آن را نشان می دهد.


آستانه گذاری
آستانه گذاری یا Thresholding برای حذف جزئیات غیرضروری از یک تصویر و تمرکز روی موارد ضروری استفاده می شود. همچنین در صورتی که شی موردنظر و پس زمینه سطوح خاکستری مشابهی داشته باشد، برای نشان دادن جزئیات پنهان مورد استفاده قرار می گیرد. آستانه را می توان بیشتر به عنوان آستانه واحد و آستانه دوگانه دسته بندی کرد. در MATLAB ، می توان آستانه گذاری واحد و دوگانه تصویر را انجام داد.
آستانه گذاری واحد
یک تصویر مقیاس خاکستری با انتخاب یک سطح خاکستری ‘T’ در تصویر اصلی ، و سپس تبدیل هر پیکسل آن به سیاه یا سفید، بسته به اینکه مقدار خاکستری آن بیشتر یا کمتر از T باشد ، به یک تصویر دودویی (سیاه و سفید) تبدیل می شود. آستانه گذاری بخش مهمی از ناحیه بندی تصویر است ، که هدف آن جداسازی اشیاء از پس زمینه است. برای تبدیل تصویر F به تصویر سیاه و سفید G با آستانه ۱۰۰ ، می توان در MATLAB از دستور G = F> 100 استفاده کرد.
مثال زیر تصویر Penguins_grey.jpg را فراخوانی می کند و هم تصویر اصلی و هم تصویر ایجاد شده پس از آستانه گذاری با آستانه ۷۰ را نمایش می دهد:
>>A = imread(‘Penguins_grey.jpg’); >>imshow(A),figure, imshow(A>70)
شکل ۱۴ و ۱۵ به ترتیب تصویر اصلی و تصویر پس از آستانه گذاری را نشان می دهد.
علاوه بر این ، یک دستور در MATLAB وجود دارد که یک تصویر مقیاس خاکستری یا یک تصویر رنگی را به تصویر سیاه و سفید تبدیل می کند. دستور im2bw(image,level) است ، که image تصویر مقیاس خاکستری است و level یک مقدار بین ۰ تا ۱ است.


آستانه گذاری دوگانه
در این حالت ، دو مقدار T1 و T2 وجود دارد و اگر سطح خاکستری بین T1 و T2 باشد، سطح آستانه با سفید شدن پیکسل انجام می شود. همچنین اگر سطح خاکستری خارج از این مقادیر آستانه باشد، پیکسل سیاه می شود.
تیز کردن تصویر
تیز کردن یا افزایش وضوح تصویر یک ابزار قدرتمند برای تأکید بر بافت های تصویر و جلب توجه بیننده است. این تکنیک می تواند کیفیت تصویر را حتی بیشتر از تصویری که در اثر ارتقاء لنز دوربین درجه یک به دست می آید ، بهبود بخشد. اکثر ابزارهای نرم افزاری برای تیز کردن تصویر با استفاده از ” unsharp mask ” کار می کنند که در واقع به منظور افزایش وضوح تصویر عمل می کند. این ابزار با افزایش اختلاف روشنایی در امتداد لبه های یک تصویر کار می کند. توجه داشته باشید که فرآیند تیز کردن قادر به بازسازی تصویر ایده آل نیست ، اما یک لبه واضح تر را ایجاد می کند.
دستور مورد استفاده برای تیزسازی تصویر در MATLAB این است:
B = imsharpen(A)
این دستور ، یک نسخه بهبودیافته از مقیاس خاکستری یا تصویر ورودی رنگی (RGB) A را برمی گرداند، که در آن ویژگی های تصویر مانند لبه ها با استفاده از روش unsharp masking تیز شده اند.
B = imsharpen(A, Name, Value,….) با استفاده از Name وValue با کنترل unsharp masking تصویر را تیز می کند.
اجازه دهید استفاده از تابع imsharpen را مشاهده کنیم:
>> a=imread(‘Image_sharpen.jpg’); >>imshow(a)
شکل ۱۶ تصویری را که باید تیز شود نشان می دهد. (Image_sharpen.jpg )

کد های زیر ، تصویر را با استفاده از دستور ساده imsharpen تیز می کنند:
>> b=imsharpen(a); >>figure,imshow(b)
شکل ۱۷ تصویر تیز شده و واضح را نشان می دهد.

شما می توانید پارامترهای ‘radius’ و ‘amount’ را در تابع imsharpen در مثال زیر مشخص کنید:
>> b=imsharpen(a,’Radius’,۴,’Amount’,۲); >>figure,imshow(b)
شکل ۱۸ تصویر بدست آمده را نشان می دهد.

همانطور که می بینید ، تصویر در شکل ۱۸ بسیار واضح تر از تصویر در شکل ۱۷ است ، که خود بسیار واضح تر از تصویر در شکل ۱۶ است.
ادامه در قسمت سوم
 مجله هوش مصنوعی شهاب
مجله هوش مصنوعی شهاب





یک نظر
دنبال کنید : پردازش تصویر با استفاده از MATLAB – قسمت سوم : فیلتر های فضایی - مجله شهاب