پردازش تصویر با استفاده از MATLAB – قسمت سوم : فیلتر های فضایی

روش های فیلتر های فضایی یا Spatial Filtering به عملیاتی گفته می شود که در آن مقدار حاصل از یک پیکسل در یک مختصات معین تابعی از مقدار پیکسل اصلی در آن نقطه و همچنین برخی از همسایگان آن پیکسل اصلی است. این عملیات شامل عملیات فیلتر خطی و عملیات فیلتر غیر خطی می شوند.

در فیلترهای خطی ، پیکسل خروجی برابر است با مجموع حاصل ضرب نقطه ای مقادیر پیکسل و ضرایب ماسک در همسایگی پیکسل اصلی در تصویر. به عبارت دیگر، اگر تابعی که توسط آن مقدار خاکستری جدید محاسبه می شود، یک تابع خطی از تمام مقادیر خاکستری موجود در ماسک باشد، فیلتر به عنوان فیلتر خطی شناخته می شود. به عنوان مثال فیلتر میانگین نمونه ای از فیلتر خطی است.

در فیلترهای غیرخطی ، پیکسل خروجی حاصل از یک توالی مرتب شده از مقادیر پیکسل در همسایگی پیکسل اصلی در تصویر انتخاب می شود. فیلتر میانه نمونه ای از فیلتر غیرخطی است.

فیلترهای خطی

کانولوشن و همبستگی دو عملیات ریاضی اساسی هستند که در فیلترهای خطی مبتنی بر الگوریتم های پردازش تصویر همسایگی محور به کار می روند.

کانولوشن

کانولوشن یک تصویر، برای هر پیکسل، یک مجموع وزن دار از مقادیر آن پیکسل و همسایگانش را پردازش می کند. بسته به انتخاب وزن های مختلف، می توان طیف گسترده ای از عملیات پردازش تصویر را از طریق کانولوشن اجرا کرد.

ماسک های کانولوشنی مختلف وقتی روی یک تصویر ورودی اعمال می شوند، نتایج متفاوتی ایجاد می کنند. این عملیات فیلترگذاری و ماسک گذاری به عنوان فیلتر فضایی نامیده می شود. فیلترهای فضایی اغلب بر اساس رفتار شان در فرکانس فضایی نامگذاری می شوند.

فیلترهای پایین گذر (LPF) آن دسته از فیلترهای فضایی هستند که تأثیر آن ها بر روی تصویر خروجی معادل کاهش مولفه های فرکانس بالا ( جزئیات ظریف در تصویر ) و حفظ مولفه های فرکانس پایین (کلیات تر و نواحی همگن در تصویر) است. این فیلترها معمولاً برای مات کردن تصویر یا کاهش میزان نویز موجود در تصویر بکار گرفته می شوند. معمولا فیلترهای پایین گذر خطی را می توان با استفاده از ماسک های کانولوشن دو بعدی با ضرایب غیر منفی پیاده سازی کرد.

فیلترهای بالاگذر (HPF) به طور مکمل و در نقطه مقابل فیلتر های پایین گذر (LPF) عمل می کنند، یعنی این فیلترها مولفه های فرکانس بالا را با اثرات احتمالی افزایش پیکسل های نویزی نیز حفظ یا بهبود می بخشند. اجزای فرکانس بالا شامل جزئیات ظریف، نقاط، خطوط و لبه ها هستند. به عبارت دیگر، این کار، تغییرات شدت روشنایی تصویر را برجسته می کند.

دو تابع در جعبه ابزار پردازش تصویر متلب (IPT) وجود دارد که می توان از آن ها برای پیاده‌سازی کانولوشن دو بعدی استفاده کرد: conv2 و filter2 .

تابع conv2 کانولوشن دو بعدی را بین دو ماتریس محاسبه می کند. به عنوان مثال، C=conv2(A,B) کانولوشن دو بعدی ماتریس های A و B را محاسبه می کند. اگر یکی از این ماتریس ها یک فیلتر دو بعدی پاسخ ضربه محدود (FIR) باشد، ماتریس دیگر در دو بعد فیلتر می شود.

تابع filter2 ماسک کانولوشن یعنی فیلتر ۲ بعدی FIR را ۱۸۰ درجه در هر جهت می چرخاند تا یک کرنل کانولوشن ایجاد کند و سپس conv2 را برای انجام عملیات کانولوشن فراخوانی می کند.

Y=filter2(h,X) داده های “X” را با فیلتر دو بعدی FIR در ماتریس “h” فیلتر می کند. نتیجه “Y” را با استفاده از همبستگی دوبعدی محاسبه می کند و قسمت مرکزی همبستگی را برمی گرداند. که به اندازه “X” است.

Y=filter2(h,X,shape) بخشی از Y را که توسط پارامتر shape مشخص شده است برمی گرداند. Shape رشته ای است با یکی مقادیر زیر تعریف می شود:

1. “full” همبستگی کامل دوبعدی را برمی گرداند. در این مورد، Y بزرگتر از X است.
2. “same” (پیش‌فرض) بخش مرکزی همبستگی را برمی‌گرداند. در این مورد، Y هم اندازهX است.
3. “valid” فقط آن بخش هایی از همبستگی را برمی گرداند که بدون لبه های دارای لایه صفر محاسبه می شوند. در این مورد، Y کوچکتر از X است.

 

در تابع filter2 هیچکدام نسبت به دیگری مزیت خاصی ندارند و بسته به مسئله می توان از هر یک استفاده کرد.

می توان فیلتر را به صورت دستی یا با استفاده از تابع fspecial ایجاد کرد. fspecial یک تابع IPT است که برای ساده سازی ساخت فیلترهای تصویر دوبعدی رایج طراحی شده است. که به صورت زیر به کار می رود:

h = fspecial(type, parameters)

که:

1. متغیر “h” ماسک فیلتر است
2. تنظیمات متغیر”type” شامل موارد مختلفی است. از جمله : “average” فیلتر میانگین‌گیری، “disk” فیلتر میانگین‌گیری دایره ای، “gaussian” فیلتر پایین‌گذر گاوسی، “laplacian” عملگر لاپلاسین دوبعدی، “log” فیلتر لاپلاسین گاوسی (LoG)، “motion” تقریبی از حرکت خطی دوربین، “prewitt” و “sobel” فیلترهای تأکید بر لبه افقی و “unsharp” فیلتر افزایش کنتراست.
3. متغیر “parameters” اختیار است و می تواند بسته به نوع فیلتر متفاوت باشد. به عنوان مثال، ابعاد ماسک، انحراف استاندارد ( برای فیلتر گاوسی ) و غیره

 

همچنین برای پیاده سازی فیلترهای خطی در متلب می توان از دستور imfilter به صورت نیز استفاده کرد:

g = imfilter(f, h, mode, boundary_options, size_options);

که f تصویر ورودی است، h ماسک یا فیلتر است، و mode می تواند ‘conv’ یا ‘corr’ باشد، که به ترتیب نشان دهنده فیلتر کردن با استفاده از کانولوشن یا همبستگی (که پیش فرض است) است.

boundary_options به نحوه برخورد الگوریتم فیلتر کردن با مقادیر حاشیه ای اشاره دارد. این نحوه برخورد شامل چهار روش است:

1. لایه گذاری با X : مرزهای آرایه ورودی که یک تصویر است با اضافه کردن مقدار “X” پر می‌شود. این گزینه پیش‌فرض است (با X=0)
2. لایه گذاری متقارن (Symmetric) : مرزهای آرایه ورودی (تصویر) با انعکاس آینه ای حاشیه تصویر پر می شود.
3. لایه گذاری تکراری (Replicate) : مرزهای تصویر ورودی با تکرار مقادیر نزدیک به حاشیه تصویر پر می شود.
4. لایه گذاری دایره ای (Circular) : مرزهای تصویر ورودی با فرض دوره ای بودن آرایه ورودی پر می شود، یعنی تصویر را به عنوان یک تابع متناوب دوبعدی در نظر می گیریم.

 

در مورد size_options، دو گزینه برای اندازه تصویر به دست آمده وجود دارد: “full” (تصویر خروجی نتیجه فیلتر کامل است، یعنی اندازه تصویر افزایش یافته یا لایه گذاری شده) یا “same” (تصویر خروجی با ورودی هم اندازه است)، که پیش فرض است. “g” هم تصویر خروجی است.

 

همبستگی : همبستگی یا Correlation همان کانولوشن است بدون قرینه کردن (چرخش) ماسک قبل از محاسبه مجموع حاصل ضرب ها. استفاده از همبستگی و کانولوشن در عملیات پردازش همسایگی دوبعدی ، اغلب تفاوت چندانی ندارد زیرا بسیاری از ماسک های پرکاربرد مورد استفاده در پردازش تصویر در حول مبدا متقارن هستند.

فیلترهای خطی پایین گذر

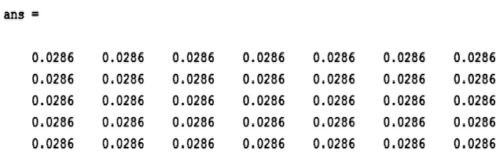
فیلتر میانگین گیری یک LPF خطی است که با استفاده از گزینه “average” در تابع fspecial قابل پیاده سازی است. دستور نوشته شده زیر یک فیلتر میانگین با اندازه ۵×۷ تولید می کند:

fspecial(‘average’, [۵,۷])

که خروجی این دستور در متلب به صورت زیر است:

همچنین کد زیر یک فیلتر میانگین با ابعاد ۳×۳ را روی تصویر Penguins_grey.jpg اعمال می کند:

A = imread(‘Penguins_grey.jpg’);
B = fspecial(‘average’);
C = filter2(B,A);
figure, imshow(A),figure, imshow(C/255)

ماتریس B یک ماتریس ۳×۳ است که هر عنصر آن دارای مقدار ۰٫۱۱۱ است. ماتریس C دارای داده هایی از نوع double است که می توانیم با تقسیم آن بر ۲۵۵ ماتریسی با مقادیر در بازه ۰-۱ داشته باشیم تا در تابع imshow از آن استفاده کنیم. هم تصویر اصلی و تصویر فیلتر شده به ترتیب در شکل های ۱ و ۲ نشان داده شده اند.

همانطور که در تصویر فیلتر شده ملاحظه می کنید، فیلتر میانگین تصویر را مات می کند و لبه های تصویر نسبت به تصویر اصلی وجه تمایز کمتری دارند. هر چه ابعاد فیلتر میانگین بزرگتر باشد، اثر مات کنندگی آن نیز بیشتر است. کد زیر عملیات میانگین گیری را با استفاده از فیلتر میانگین ۹×۹ نشان می دهد:

A = imread(‘Penguins_grey.jpg’);
B = fspecial(‘average’,[۹,۹]);
C = filter2(B,A);
figure, imshow(A),figure, imshow(C/255)

شکل ۳ تصویر فیلتر شده را نشان می دهد.

فیلتر میانگین یک فیلتر میانگین گیری حسابی است. انواع دیگر فیلترهای میانگین عبارتند از فیلترهای میانگین هندسی، فیلترهای میانگین harmonic و فیلترهای میانگین contra-harmonic. فیلتر میانگین ساده ترین و پرکاربردترین فیلتر هموارکننده فضایی است.

فیلتر میانگین با استفاده از یک پنجره لغزان به ابعاد mxn و محاسبه میانگین تمام مقادیر پیکسل در پنجره و در نهایت جایگزینی این مقدار محاسبه شده با پیکسل مرکزی در تصویر، عمیلات میانگین گیری تصویر را انجام می دهد.

همانطور که در بالا اشاره شد، فیلتر میانگین متناسب با اندازه پنجره ، باعث ایجاد یک مات شدگی در تصویر می شود، که البته این مات شدگی به کاهش نویز، به ویژه نویز گاوسی یا یکنواخت کمک می کند. به عنوان مثال، نویز فلفل نمکی را به تصویر Penguins_grey.jpg اضافه کرده و آن را با استفاده از فیلتر میانگین فیلتر می کنیم. نویز فلفل نمکی باعث ایجاد نقاط مجزا بسیار روشن (نمک) و بسیار تیره (فلفل) در یک تصویر می شود.

دستور اضافه کردن نویز فلفل نمکی به تصویر به صورت زیر است:

A = imread(‘Penguins_grey.jpg’);
Noise_snp=imnoise(A,’salt & pepper’);
imshow(Noise_snp)

 

شکل ۴ تصویر Penguins_grey.jpg را با نویز فلفل نمکی نشان می دهد.

دستورات زیر نویز فلفل نمکی را از شکل ۴ حذف می کنند:

>> B = fspecial(‘average’, [۹,۹]);
>> C = filter2(B,Noise_snp);
>>imshow(C/255)

 

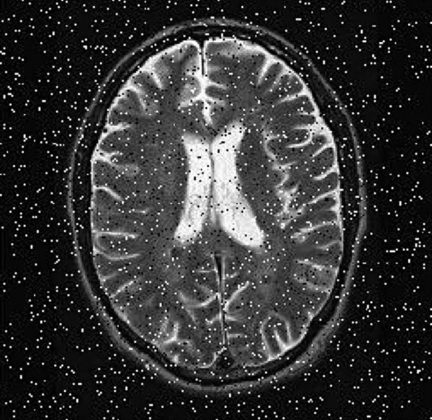
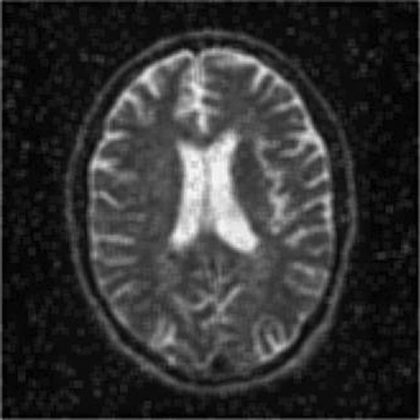
شکل ۵ تصویر حاصل را نشان می دهد. همانطور که ملاحظه می کنید، تصویر در شکل ۵ مات شده اما نویز فلفل نمکی آن حذف شده است. در شکل ۶ تصویر دیگری ( تصویر MRI ) با نویز فلفل نمکی و شکل ۷ تصویر را پس از اعمال عملیات زیر نشان می دهد:

>> a=imread(‘MRI_snp.jpg’);
>>imshow(a)
>> B = fspecial(‘average’, [۹,۹]);
>> C = filter2(B,a);
>>imshow(C/255)

 

نوع دیگری از فیلتر میانگین حسابی، فیلتر میانگین هندسی است که در درجه اول در تصاویر با نویز گاوسی استفاده می شود. در واقع گفته می شود که این فیلتر جزئیات تصویر را بهتر از فیلتر میانگین حسابی حفظ می کند.

فیلترهای گاوسی نیز نوع دیگری از فیلترهای خطی هستند. این ها فیلترها پایین گذر هستند که بر اساس تابع توزیع احتمال گاوسی به صورت زیر تعریف می شوند که در آنσ  انحراف معیار است :

ƒ(x)=e^–x2/2σ۲

فیلترهای گاوسی دارای اثر مات کنندگی هستند که به نظر بسیار شبیه به آن چیزی است که توسط میانگین همسایه ها ایجاد می شود.

دستورات زیر فیلتر گاوسی را روی تصویر Penguins_grey.jpg اعمال می کنند:

>> A = imread(‘Penguins_grey.jpg’);
>> G1=fspecial(‘gaussian’,[۱۱,۱۱]);
>> G1image=filter2(G1,A)/256;
>>imshow(G1image)

اعداد داخل براکت اندازه فیلتر را نشان می دهند که مقدار پیش فرض آن ۳×۳ است. پارامتر آخر هم انحراف معیار است که اگر مقداری مشخص نشده باشد، مقدار پیش فرض ۰٫۵ در نظر گرفته می شود. در دستور بالا، از آنجایی که پارامتر انحراف معیار مشخص نشده است، مقدار پیش فرض ۰٫۵ گرفته می شود.

شکل ۸ یک تصویر فیلتر شده گاوسی را با مقدار انحراف معیار ۰٫۵ نشان می دهد.

هنگامی که انحراف معیار به ۵ تنظیم شود، همانطور که در دستور نشان داده شده است (G1=fspecial(‘gaussian’,[11,11],5)؛ تصویر حاصل مانند شکل ۹ نشان داده شده است.

فیلترهای خطی بالا گذر

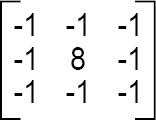
HPF های خطی را می توان با استفاده از ماسک های کانولوشن دوبعدی با ضرایب مثبت و منفی، که مربوط به تقریب دیجیتالی لاپلاسین است – یک مشتق مرتبه دوم ساده و ایزوتروپیک ( تغییرناپذیر با چرخش ) که به تغییر شدت روشنایی در هر جهت واکنش نشان می دهد – پیاده سازی کرد.

یک پیاده سازی دیجیتال جایگزین لاپلاسین، تمام هشت همسایه پیکسل اصلی تصویر ورودی را در نظر می گیرد و می تواند توسط ماسک کانولوشنی زیر پیاده سازی شود:

فیلترهای اختلاف جهت دار

فیلترهای اختلاف جهت دار مشابه فیلتر فرکانس بالا لاپلاسین هستند اما بر لبه ها در یک جهت خاص تاکید دارند. این فیلترها معمولاً فیلترهای emboss نامیده می شوند و شامل چهار ماسک هستند که می توان برای اجرای برجستگی تصویر از آن ها استفاده کرد:

فیلترهای خطی بالا گذر شامل عملگرهای Prewitt و Sobel هستند. به این روش ها ، روش های تشخیص لبه مرتبه اول نیز گفته می شود. فیلترهای بالا گذر همچنین برای عملیات تشخیص لبه و تقویت لبه استفاده می شود.

تابع edge دارای گزینه هایی برای عملگر های Prewitt و Sobel است. تشخیص لبه با استفاده از عملگرهای Prewitt و Sobel نیز می تواند با استفاده از دستور imfilter با ماسک های ۳×۳ مربوطه (که می تواند با استفاده از دستور fspecial ایجاد شود) حاصل شود.

کد زیر لبه های تصویر را با استفاده از عملگر Prewitt استخراج می کند:

>> A = imread(‘Penguins_grey.jpg’);
>>Prewitt_A=edge(A,’Prewitt’);
>>imshow(Prewitt_A)

شکل ۱۰ تصویر نتیجه را نشان می دهد.

حال اجازه دهید نویز گاوسی را به تصویر Penguins_grey.jpg اضافه کنیم. سپس آن را با استفاده از آشکارساز لبه Prewitt پردازش می کنیم:

>> A = imread(‘Penguins_grey.jpg’);
>>A_noise=imnoise(A,’gaussian’);
>>Prewitt_A_noise=edge(A_noise,
’Prewitt’);
>>imshow(A_noise)
>>imshow(Prewitt_A_noise)

شکل ۱۱ تصویر را با نویز گاوسی اضافه شده و شکل ۱۲ تصویر فیلتر شده با آشکارساز لبه Prewitt را نشان می دهد.

کد زیر مربوط به استفاده از عملگر Sobel برای تشخیص لبه است و شکل ۱۳ تصویر حاصل را نشان می دهد.

>> A = imread(‘Penguins_grey.jpg’);
>>Sobel_A=edge(A,’sobel’);
>>imshow(Sobel_A)

 

حال اجازه دهید نویز گاوسی را به تصویر Penguins_grey.jpg اضافه کنیم. سپس آن را با استفاده از آشکارساز لبه Sobel پردازش می کنیم:

>> A = imread(‘Penguins_grey.jpg’);
>>A_noise=imnoise(A,’gaussian’);
>>Sobel_A=edge(A,’sobel’);
>>imshow(Sobel_A)

شکل ۱۴ تصویر حاصل را نشان می دهد.

فیلترهای غیرخطی

فیلترهای غیرخطی در سطح همسایگی کار می کنند، اما مقادیر پیکسل را با استفاده از عملگر کانولوشن پردازش نمی کنند. در عوض، این فیلتر ها معمولاً یک تابع رتبه بندی یا مرتب سازی را به مقادیر پیکسل در همسایگی اعمال می کنند و یک مقدار را از لیست مرتب شده انتخاب می کنند. به همین دلیل، به آن ها فیلترهای رتبه بندی هم می گویند. نمونه هایی از فیلترهای غیرخطی عبارتند از فیلتر میانه و فیلترهای حداکثر و حداقل.

فیلتر میانه یک فیلتر غیرخطی پرکاربرد است که در پردازش تصویر مورد استفاده قرار می گیرد. این فیلتر با مرتب کردن مقادیر پیکسل در یک همسایگی، یافتن مقدار میانه و جایگزینی آن با مقدار پیکسل اصلی در آن همسایگی کار می کند. فیلتر میانه در کاهش نویز فلفل نمکی بسیار بهتر از یک فیلتر میانگین ​​با اندازه همسایگی برابر عمل می کند. فیلتر میانه را می توان در متلب با تابع medfilt2 که توسط IPT ارائه شده است اعمال کرد.

کد زیر استفاده از فیلتر میانه را برای حذف نویز فلفل نمکی از تصویر Penguins_grey.jpg نشان می دهد:

A = imread(‘Penguins_grey.jpg’);
Noise_snp=imnoise(A,’salt& pepper’);
imshow(Noise_snp)
Filtered_snp=medfilt2(Noise_snp,[3 3]);
imshow(Filtered_snp)

شکل ۱۵ و ۱۶ به ترتیب تصاویر نویزی و حذف نویز شده را نشان می دهند. شکل ۱۷ نیز تصویر نویزی دیگری را نشان می دهد که نتیجه حذف نویز شده آن با استفاده از فیلتر میانه در شکل ۱۸ ارائه شده است.

پنجره لغزان

عملیات همسایگی پنجره لغزان در IPT با استفاده از یکی از این دو تابع پیاده سازی می شود: nlfilter یاcolfilt  . هر دو تابع یک تابع تعریف شده توسط کاربر را به عنوان پارامتر می پذیرند. چنین تابعی می تواند عملیات خطی و همچنین غیرخطی را بر روی پیکسل های یک پنجره اعمال کند. برای فیلترهای رتبه بندی مانند فیلترهای حداقل، حداکثر و میانه ، تابع ordfilt2 بسیار مناسب تر هستند.

برای استفاده از تابع nlfilter از سه آرگومان استفاده می کنیم: ماتریس تصویر، اندازه فیلتر و تابعی که باید اعمال شود. خط زیر فیلتری را تعریف می کند که حداکثر مقدار را در یک محله ۳×۳ نتیجه می دهد :

cmax = nlfilter(c,[3,3],‘max(x(:))’);

فیلتری که حداقل مقدار را در یک همسایگی ۳×۳ بر می گرداند با دستور زیر تعریف می شود:

cmin = nlfilter(c,[3,3],‘min(x(:))’);

پردازش ناحیه مورد نظر

گاهی اوقات عملیات فیلتر کردن فقط در قسمت کوچکی از تصویر انجام می گیرد که به آن ناحیه مورد نظر یاROI  گفته می شود. ROI با تعریف یک ماسک مشخص می شود کهتصویر اصلی را به بخشی از تصویر که قرار است عملیات در آن انجام شود محدود می کند.

ماسک گذاری تصویر ، فرآیند استخراج یک تصویر فرعی از یک تصویر بزرگتر برای پردازش بعدی است. پردازش ROI را می توان با استفاده از ترکیبی از دو تابع در MATLAB پیاده سازی کرد: roipoly ( برای ماسک گذاری تصویر ) و roifilt2 ( برای پردازش ROI انتخاب شده ).

امیدواریم این آموزش برای شما مفید بوده باشد. در قسمت بعد، در مورد روش های رفع ماتی تصویر در متلب صحبت خواهیم کرد.

منبع Electronics Foru