در ابتدای جزوه ای که برای قبولی در درس تئوری آمار استفاده کردم، نویسندگان (جورج ساسلا و راجر برگر) در مقدمه توضیح دادند که چرا آن ها تصمیم گرفتند یک جزوه بنویسند:
” زمانی که یک نفر می فهمد که شما یک جزوه را می نویسید، یکی از این دو سوال پرسیده خواهد شد. اولی این است که ” چرا یک جزوه می نویسید؟ و دومین موضوع این است که چه چیزی جزوه ی شما را با بقیه جزوه های موجود متفاوت می کند؟ ” پاسخ سوال اول نسبتاً آسان است. شما در حال نوشتن یک جزوه هستید، زیرا شما از جزوه های موجود راضی نیستید.”
من منطق نویسندگان را در اینجا اعمال می کنم. تحلیل مولفه های اصلی (PCA) یک تکنیک مهمی در زمینه آمار و علوم داده ها است که باید درک شود … اما هنگامی که به دانش آموزان کلاس General Assembly درس می دادم، من متوجه شده ام که منابع آنلاین خیلی تکنیکی هستند ، به طور کامل به نیازهای ما پاسخ نمی دهند، و / یا اطلاعات متناقض ارائه می کنند. می توانم بگویم که من از جزوات موجود راضی نیستم.
در نتیجه، من می خواستم پاسخ سوالات “چی”، “چه زمانی” و “چطور” و “چرا” در مورد روش تحلیل مولفه های اصلی و همچنین پیوند هایی با برخی از منابع که می تواند به توضیح بیشتر این موضوع کمک کند، را کنار هم قرار دهم. مخصوصا می خواهم منطق این روش، ریاضی پشت آن، برخی از بهترین روش ها و اشکالات بالقوه این روش را ارائه کنم.
فهرست مطالب
در حالی که من می خواهم تا آنجا که ممکن است، تحلیل مولفه های اصلی را به صورت قابل فهم ارائه کنم، اما الگوریتمی که ما می خواهیم بررسی کنیم بسیار فنی است. آشنا بودن با برخی (یا همه ی) این مواردی که در ادامه گفته شده، فهم این مطلب و روش تحلیل مولفه های اصلی را آسان تر می کند : عملیات ماتریس / جبر خطی ( ضرب ماتریس ، جابجایی ماتریس ، ماتریس معکوس ، تجزیه ماتریس ، بردار های ویژه و مقادیر ویژه ) و آمار / یادگیری ماشین ( استاندارد سازی ، واریانس ، کوواریانس ، مستقل بودن ، رگرسیون خطی ، انتخاب ویژگی ). من پیوند های مربوط به این موضوعات را در طول متن آورده ام، اما امیدوارم که این موارد به جای نیازمندی برای فهمیدن این مقاله به عنوان یک یادآور عمل کنند.
تحلیل مولفه های اصلی (PCA) چیست؟
بگذارید بگوییم که می خواهید میزان افزایش تولید ناخالص داخلی برای سال ۲۰۱۷ را پیش بینی کنید. شما اطلاعات زیادی در دسترس دارید : تولید ناخالص داخلی برای سه ماهه اول تولید ناخالص ملی ، تولید ناخالص ملی برای کل سال ۲۰۱۶ و ۲۰۱۵ و غیره. شما هر شاخص اقتصادی در دسترس عموم مانند نرخ بیکاری ، نرخ تورم و غیره را دارید. شما داده های سرشماری سالانه که برآورد می کند چه تعداد از شهروندان در هر صنعت کار می کنند. شما می دانید که چند نفر از اعضای مجلس و سنا به هر حزب سیاسی تعلق دارند. اطلاعات قیمت سهام، تعداد عرضه اولیه سهام در هر سال، و و تعداد مدیر عامل هایی که می خواهند وارد مجلس عوام شوند. با وجود تعداد زیادی از متغیر ها، این تنها بخش کوچکی از آن است.
به طور خلاصه شما اطلاعات بی شماری دارید.
اگر قبلاً با متغیر های زیادی کار کرده اید، می دانید که این می تواند مشکلاتی را به وجود بیاورد. آیا روابط بین هر متغیر را درک می کنید؟ آیا شما متغیر های زیادی دارید که شما را در خطر بیش برازش مدل خود قرار می دهند و یا اینکه فرضیات روش مدلسازی ای که استفاده می کنید را نقض می کنید؟
ممکن است این سوال را بپرسید که : ” من چگونه تمام متغیر های جمع آوری شده را در نظر بگیرم و بر روی تعداد کمی از آن ها تمرکز می کنم؟ در شرایط فنی، شما می خواهید ابعاد فضای ویژگی خود را کاهش دهید. با کاهش ابعاد فضای ویژگی، روابط کمتری بین متغیر ها وجود دارد که می توانید در نظر بگیرید و به احتمال کمتری مدل خود بیش برازش می کنید. (توجه : به این معنی نیست که مشکل بیش برازش دیگر اتفاق نمی افتد ، اما ما به سمت درستی حرکت می کنیم!)
تعجبی ندارد که کاهش ابعاد فضای ویژگی، کاهش ابعادی نامیده می شود. روش های زیادی برای کاهش ابعاد وجوددارد، اما اغلب این روش ها به یکی از این دو دسته تقسیم می شوند:
- حذف ویژگی
- استخراج ویژگی
حذف ویژگی همان چیزی است که به نظر می رسد: ما فضای ویژگی را با حذف مشخصه ها کاهش می دهیم. در مثال تولید ناخالص داخلی بالا، به جای در نظر گرفتن هر یک از متغیر ها، ممکن است همه متغیر ها به جز سه متغیر که فکر می کنیم بهترین تاثیر را برای رسیدن به تولید ناخالص داخلی دارند را حذف کنیم. مزایای روش های حذف ویژگی شامل سادگی و حفظ تفسیر متغیر های شما است.
به عنوان عیب این روش، شما هیچ اطلاعاتی از آن متغیر هایی که حذف کرده اید کسب نمی کنید. اگر ما تنها از تولید ناخالص داخلی سال گذشته، نسبت جمعیت در تولید مشاغل به ازای نظرسنجی های اخیر جامعه ، و نرخ بیکاری برای پیش بینی تولید ناخالص داخلی سال جاری استفاده کنیم، ما به هر آنچه که متغیر های حذف شده ممکن است به مدل ما کمک کنند، دسترسی نداریم. با حذف مشخصه ها، ما تمام سودی که متغیر های حذف شده می توانند به ما دهند را حذف کرده ایم.
اما استخراج ویژگی به این به این مشکل نمی خورد. بگذارید بگوییم ما ده متغیر مستقل داریم. در
استخراج ویژگی، ۱۰ متغیر مستقل ” جدید ” ایجاد می کنیم که هر متغیر مستقل ” جدید ” ترکیبی از هر ده متغیر مستقل “قدیمی ” است. با این حال، ما این متغیر های مستقل جدید را به روشی خاص ایجاد کرده و این متغیر های جدید را بر اساس چگونگی پیش بینی متغیر وابسته ما، ترتیب می دهیم.
ممکن است بگویید: ” کاهش ابعاد کجا وارد بازی می شود؟ ” خب، ما هر تعداد از متغیر های مستقل را که می خواهیم، حفظ می کنیم، اما ما ” کم اهمیت ترین ” را حذف می کنیم. ” از آنجا که ما متغیر های جدید را بر اساس ای که کدام یک بهتر متغیر وابسته ما را پیش بینی می کنند، ترتیب دادیم، می دانیم کدام متغیر مهم ترین و کدام یک کم اهمیت ترین متغیر است. اما به این دلیل که این متغیر های مستقل جدید ترکیبی از متغیر های قدیمی ما هستند، ما هنوز ارزشمند ترین قسمت های متغیر های قدیمی مان را حفظ می کنیم، حتی زمانی که یک یا چندمتغیر ” جدید ” را حذف می کنیم!
تحلیل مولفه های اصلی تکنیکی برای استخراج ویژگی است؛ بنابراین متغیر های ورودی ما را به یک روش خاص ترکیب می کند، سپس می توانیم “کم اهمیت ترین ” متغیر ها را حذف کنیم در حالی که هنوز ارزشمند ترین قسمت های تمام متغیر ها را حفظ می کنیم. هر یک از متغیر های ” جدید ” بعد از PCA همگی مستقل از یکدیگر هستند. این یک مزیت است زیرا فرضیات مدل خطی نیازمند این است که متغیر های مستقل ما از یک دیگر مستقل باقی بمانند. اگرتصمیم بگیریم که یک مدل رگرسیون خطی را با این متغیر های ” جدید ” برازش کنیم ( ” رگرسیون مولفه های اصلی ” را در ادامه ببینید )، این فرض لزوماً ارضا خواهد شد.
چه زمانی باید از PCA استفاده کنیم؟
- آیا می خواهید تعداد متغیر ها را کاهش دهید، اما قادر به شناسایی متغیر ها برای حذف کامل از معادلات نیستید؟
- آیا می خواهید مطمئن شوید که متغیر ها مستقل از یکدیگر هستند؟
- آیا مایل هستید که متغیر های مستقل خود را کم تر تفسیر پذیر کنید؟
اگر پاسخ شما به هر سه سوال مثبت است، PCA روش خوبی برای استفاده است. اگر به سوال ۳ ” نه ” پاسخ دهید، نباید از PCA استفاده کنید.
PCA چگونه کار می کند؟
بخش بعدی به این بحث می پردازد که چراPCA عمل می کند، اما قبل از پرش به الگوریتم جمع بندی کوتاهی می تواند برای درک مفهوم مفید باشد:
- ما می خواهیم ماتریسی را محاسبه کنیم که نشان می دهد چگونه متغیر های ما همگی با یکدیگر مرتبط هستند.
- پس از آن ما ماتریس را به دو مولفه جداگانه تقسیم می کنیم : جهت و اندازه. سپس می توانیم ” جهت ” های داده ها و ” اندازه ” ی آن ( یا اینکه هر ” جهت ” چقدر مهم است ) را بشناسیم. عکس زیر، از برنامه ی io دو جهت اصلی این داده ها را نشان می دهد. ” جهت قرمز ” و ” جهت سبز “. در این مورد ” جهت قرمز ” از اهمیت بیشتری برخوردار است. ما در ادامه به این نتیجه خواهیم رسید که چرا این چنین است، اما با توجه به اینکه چگونه این نقاط مرتب شده اند، می توانید حدس بزنید چرا ” جهت قرمز ” مهم تر از ” جهت سبز ” است؟ (راهنمایی: چه چیزی برای برازش این داده ها مناسب است؟)
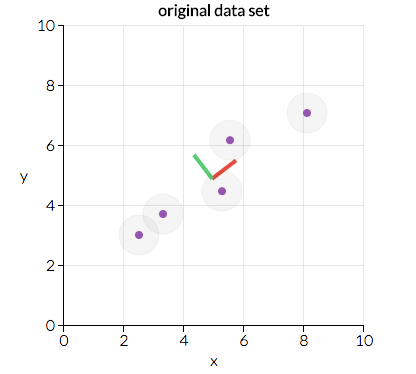
- ما داده های اصلی خود را برای همسو شدن با این جهت های مهم ( که ترکیبی از متغیر های اصلی ما هستند ) تبدیل خواهیم کرد. عکس زیر ( باز هم از setosa.io ) همان داده های بالا است، اما تبدیل شده تا محور های x و y اکنون “جهت قرمز” و “جهت سبز” باشند. اکنون بهترین خط برازش چگونه باید باشد؟
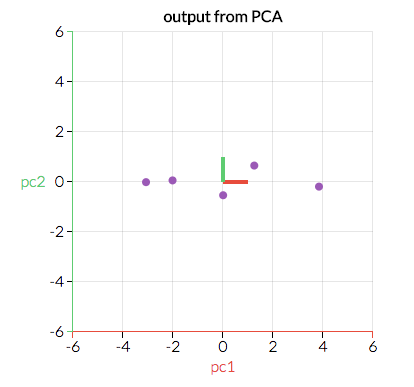
در حالیکه مثال بصری اینجا دو بعدی است (و بنابراین ما دو جهت داریم)، موردی را در نظر بگیرید که در آن داده های ما ابعاد بیشتری دارند. با مشخص کردن این که کدام “جهت” “مهم ترین” است، می توانیم داده های خود را با حذف “جهت” های “کم اهمیت” به یک فضای کوچک تر کاهش دهیم. با نمایش داده ها در فضایی کوچک تر، می توانیم ابعاد فضای ویژگی ها را کاهش دهیم… اما به این دلیل که ما داده را در این “جهت” های متفاوت تغییر داده ایم، مطمئن می شویم که تمام متغیر های اصلی را در مدل خود نگه داشته ایم!
در اینجا، من یک الگوریتم برای انجام PCA را بررسی می کنم. سعی می کنم از بیش از حد فنی بودن اجتناب کنم، اما نادیده گرفتن جزئیات در اینجا غیر ممکن است، بنابراین هدف من این است که تا حد ممکن به صورت صریح همه چیز را بررسی کنم. یک درک عمیق تر از این که چرا الگوریتم کار می کند در بخش بعدی ارائه شده است.
قبل از شروع، شما باید داده های جدولی را با n سطر و احتمال p+1 ستون داشته باشید، که در آن یک ستون متناظر با متغیر وابسته شما می باشد (معمولا با متغیر های Yنمایش داده می شود) و p ستون دیگر متناظر با هر یک از متغیر های مستقل شما است (ماتریسی که معمولاً با X مشخص می شود).
- اگر یک متغیر Y وجود داشته باشد و بخشی از اطلاعات شما باشد، آنگاه داده ها را به Y و X تفکیک کنید، همانطور که در بالا تعریف شده است. ما اغلب با X کار خواهیم کرد. (توجه: اگر هیچ ستونی برای Y وجود نداشته باشد، مشکلی نیست؛ به بخش بعدی بروید!)
- ماتریس متغیر های مستقل X را در نظر بگیرید ، و به ازا هر ستون ، میانگین این ستون را از هر ورودی کم کنید. (این تضمین می کند که هر ستون میانگین صفر دارد)
- تصمیم بگیرید که آیا داده ها را استاندارد کنید یا خیر. با توجه به ستون های X، آیا ویژگی هایی با واریانس بالاتر مهم تر از ویژگی هایی با واریانس کم تر هستند، یا اهمیت ویژگی های مستقل از واریانس است؟ (در این مورد، اهمیت به معنی این است که این ویژگی چقدر خوب Y را پیش بینی می کند) اگر اهمیت ویژگی ها مستقل از واریانس ویژگی ها باشد، پس هر مورد در ستون را بر انحراف استاندارد ستون تقسیم کنید. (ترکیب این بامرحله ۲، هر ستون X را استاندارد می کند تا اطمینان حاصل کند که هر ستون میانگین صفر و انحراف استاندارد ۱ دارد). این ماتریس محور ( و احتمالاً استاندارد) را ماتریسZ بنامید.
- ماتریس z را در نظر بگیرید. آن را ترانهاده کنید، و ماتریس ترانهاده را در ماتریس Z ضرب کنید. (نوشتن این مطلب از نظر ریاضی، به صورت ZᵀZ خواهد بود.) ماتریس حاصله کوواریانس ماتریس Z خواهد بود.
- (این احتمالاً سخت ترین گام خواهد بود. پس دقت کنید.) بردارهای ویژه و مقادیر ویژه متناظر آن ها در ZᵀZ را محاسبه کنید. این کار به راحتی در اکثر بسته های محاسباتی انجام می شود – در واقع، تجزیه ویژه ی ZᵀZ وقتی است که ما ZᵀZ را به PDP⁻¹ تبدیل می کنیم، که در آن P ماتریس بردار های ویژه است و D ماتریس موربی است که مقادیر ویژه بر روی خط مورب و بقیه ی مقادیر آن صفر می باشد. مقادیر ویژه ی ماتریس مورب D با مقادیر متناظر در ستون P مرتبط هستند – یعنی مولفه اول D ، λ₁ است و با بردار ویژه اولین ستون P متناظر است. این برای همه عناصر D و بردار های ویژه متناظر آن ها درP صادق است. ما همیشه می توانیم PDP⁻¹ را در با روش محاسبه کنیم. ( بیشتر بدانید: برای کسانی که علاقه مند هستند، ماهمیشه می توانیم PDP⁻¹ را در این روش محاسبه کنیم زیرا ZᵀZ یک ماتریس متقارن، مثبت نیمه قطعی است.)
- مقادیر ویژه λ₁, λ₂, …, λpرا در نظر بگیرید و آن ها را از بزرگ به کوچک مرتب کنید. در انجام این کار، بردار های ویژه در P را نیز به همین صورت مرتب کنید. (برای مثال، اگر λ₂ بیشترین مقدار ویژه باشد، پس ستون دوم P را بگیرید و آن را در موقعیت ستون اول قرار دهید.) با توجه به بسته محاسباتی، این کار ممکن است به صورت خودکار انجام شود. این ماتریس مرتب شده بردارهای ویژه را P* بنامید. (ستون های P* باید همانند ستون های p باشند، اما شاید به ترتیب متفاوتی قرار گرفته باشند.) توجه داشته باشید که این بردارهای ویژه مستقل از یک دیگر هستند.
مقدار Z* = ZP* را محاسبه کنید. این ماتریس جدید که Z* نامیده شده، نسخه ی استاندارد شده و مرکزی ماتریس X است اما هر مولفه از ترکیب دو متغیر اصلی بدست آمده که وزن آن ها توسط مقادیر ویژه محاسبه می شود. به عنوان یک مورد اضافه، چون بردارهای ویژه ما در P* مستقل از یک دیگر هستند، هر ستون Z* هم مستقل از یکدیگر است!
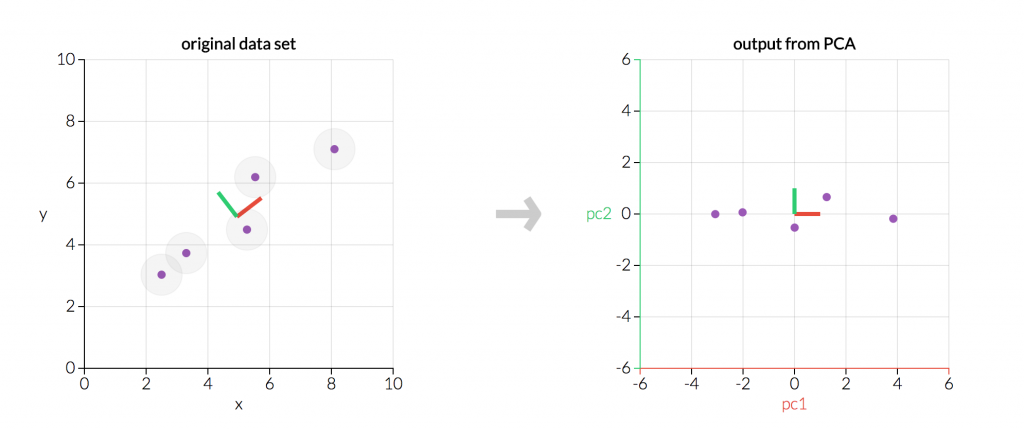
در این نمودار دو چیز را در نظر بگیرید :
- دو نمودار داده های مشابه را نشان می دهند، اما نمودار سمت راست نشان دهنده داده های اصلی تبدیل شده است به طوری که محور ما هم اکنون مولفه های اصلی است.
در هر دو گراف، مولفه های اصلی عمود بر یکدیگر هستند. در واقع، هر مولفه ی اصلی همیشه با تمام مولفه های اصلی دیگر متعامد (عبارت ریاضی رسمی برای عمود بودن دو مولفه) خواهد بود. (اگر باور نمی کنید می توانید در این برنامه آزمایش کنید.)
از آنجا که مولفه های اصلی ما متعامد یکدیگر هستند، ازنظر آماری مستقل از یکدیگر هستند … به همین دلیل ستون های Z* به صورت خطی مستقل از یکدیگر هستند!
- در نهایت، ما باید مشخص کنیم که چند ویژگی را باید نگه داریم و چند ویژگی باید حذف شود. سه روش معمول برای تعیین این موضوع وجود دارد که در زیر آورده شده است و با یک مثال واضح نشان داده شده اند:
- روش ۱ : ما به طور دل خواه تعداد ابعادی که می خواهیم نگه داریم را انتخاب می کنیم. شاید من می خواهم به طور بصری چیز ها را در دو بعد نشان دهم، به همین خاطر فقط دو ویژگی را نگه می دارم. این روش بسته به نوع کار دارد و قانون سخت و سریعی برای تعیین اینکه چند ویژگی باید داشته باشیم، وجود ندارد.
- روش ۲ : نسبت واریانس توضیح داده شده (به طور خلاصه در ادامه توضیح داده شده) را برای هر ویژگی محاسبه کنید، یک آستانه در نظر بگیرید، و ویژگی ها را اضافه کنید تا به آن آستانه برسید.(برای مثال، اگر می خواهید ۸۰% از تغییرات کل را که احتمالاً توسط مدل شما توضیح داده می شود، را توضیح دهید، ویژگی هایی با بزرگ ترین نسبت واریانس توضیح داده شده را اضافه کنید تا زمانی که نسبت واریانس توضیح داده شده به ۸۰% برسد. )
- روش ۳ : این روش ارتباط نزدیکی با روش ۲ دارد. نسبت واریانس توضیح داده شده برای هر ویژگی را محاسبه کنید، ویژگی ها را بر اساس نسبت واریانس توضیح داده شده مرتب کنید و نمودار نسبت تجمعی واریانس توضیح داده شده را در حالی که ویژگی های بیشتری را نگه می دارید، رسم کنید. (این طرح یک نموار سنگ ریزه نامیده می شود که در ادامه نشان داده شده است.) می توان با شناسایی نقطه ای که افت قابل توجهی در واریانس توضیح داده شده نسبت به ویژگی قبلی ایجاد می کند و انتخاب ویژگی ها تا آن نقطه، هر تعداد دلخواه ویژگی را اضافه کرد.(من این را ” پیدا کردن آرنج ” می نامم، به طوری که “خم ” یا ” آرنج ” را در نمودار سنگ ریزه نشان دهنده ی جایی است که بیشترین افت در نسبت واریانس توضیح داده شده اتفاق می افتد.)
از آنجا که هر مقدار ویژه به طور تقریبی اهمیت بردار ویژه متناظر آن است، نسبت واریانس توضیح داده شده، مجموع مقادیر ویژه ویژگی ها است که به صورت مجموع مقادیر ویژه جدا کرده اید.
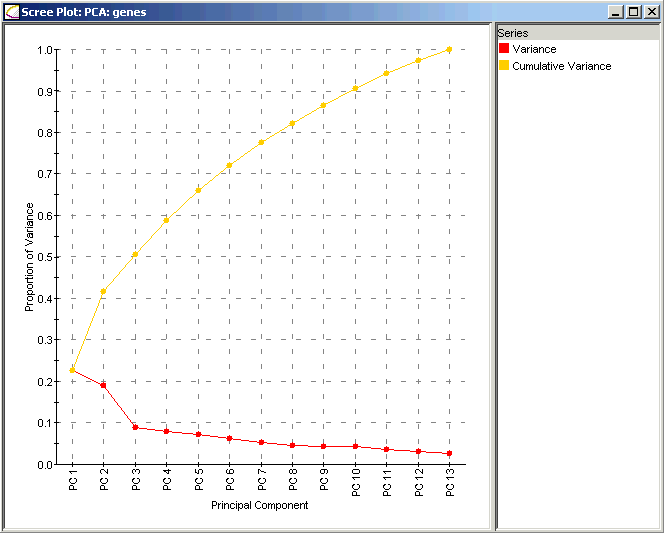
این نمودار سنگ ریزه را برای داده های ژنتیک در نظر بگیرید (منبع). خط قرمز نشان دهنده ی نسبت واریانس توضیح داده شده برای هر ویژگی است، که از طریق تقسیم مقدار ویژه ی مولفه ی اصلی بر جمع تمام مولفه های اصلی به دست می آید. نسبت واریانس توضیح داده شده ی مولفه اصلی تنها با در نظر گرفتن مولفه ی ۱ به صورت λ₁/(λ₁ + λ₂ + … + λp) می شود ک حدود ۲۳% می باشد. نسبت واریانس توضیح داده شده مولفه اصلی تنها با در نظر گرفتن مولفه ی ۲ به صورت λ₂/(λ₁ + λ₂ + … + λp) است که حدود ۱۹% می شود.
نسبت واریانس توضیح داده شده مولفه اصلی با در نظر گرفتن دو مولفه ی ۱ و ۲ به صورت (λ₁ + λ₂)/(λ₁ + λ₂ + … + λp) است که حدود ۴۲% می شود.این جایی است که خط زرد وارد می شود؛ خط زرد نشان دهنده نسبت تجمعی واریانس توضیح داده شده است اگر تمام مولفه های اصلی تا آن نقطه را در نظر گرفته باشید. برای مثال، نقطه زرد بالای PC2 نشان می دهد که در نظر گرفتن دو مولفه ی اصلی ۱ و ۲ حدود ۴۲% میزان کل واریانس در مدل را توضیح می دهد.
حال بگذارید چند مثال بزنیم:
- روش ۱ : ما به طور دل خواه تعدادی از مولفه های اصلی را انتخاب می کنیم. فرض کنید من می خواستم پنج مولفه اصلی را در مدل خود نگه دارم. در مورد داده های ژنتیکی بالا، این پنج مولفه اصلی حدود ۶۶% درصد از تغییرات کل را توضیح می دهد که توسط تمام ۱۳ مولفه های اصلی تشریح می شود.
- روش ۲ : فرض کنیم می خواهیم به قدری مولفه ی اصلی اضافه کنیم تا ۹۰% از تنوع پذیری کل به وسیله ی ۱۳ مولفه ی اصلی توضیح داده شود. در مورد داده های ژنتیکی بالا، من ۱۰ مولفه ی اصلی را ابتدا اضافه می کنم و سه مولفه ی آخر را از Z* بگیرم.
روش ۳ : اینجا می خواهیم “آرنج را پیدا کنیم”. در نمودار سنگ ریزه ی بالا، شاهد افت زیاد نسبت تغییر پذیری توضیح داده شده بین مولفه ی اصلی ۲ و مولفه ی اصلی ۳ هستیم. در این حالت ممکن است بخواهیم دو ویژگی اول را شامل شود و ویژگی های باقی مانده را حذف کنیم. همانطور که می بینید، این روش کمی ذهنی است چون ” آرنج ” تعریف دقیقی از نظر ریاضی ندارد و در این مورد، ما مدلی می حواهیم که تنها در حدود ۴۲% کل تغییرات را توضیح می دهد.
(توجه : بعضی از نمودار های سنگ ریزه بجای نسبت واریانس، اندازه بردارهای ویژه را در محور Y نسبت دارند. این امر منجر به نتایج معادل می شود، اما نیازمند محاسبه دستی نسبت واریانس است.)
زمانی که ما متغیر های تبدیل شده ای که میخواهیم حذف کنیم را حذف کردیم، کار ما تمام می شود! این PCA است.
اما واقعا “چرا” PCA کار می کند؟
در حالی که PCA یک روش بسیار تکنیکی با تکیه بر الگوریتم های جبر خطی عمیق می باشد، وقتی به آن فکر کنید، یک روش نسبتا شهودی است.
- اول، ماتریس کوواریانس ZᵀZ یک ماتریس است که شامل برآورد میزان هر متغیر در Z نسبت به سایر متغیر های Z است. درک چگونگی ارتباط یک متغیر با دیگر متغیر ها بسیار مهم است.
دوم، مقادیر ویژه و بردار های ویژه مهم هستند. بردار های ویژه جهات رانشان می دهند. به طراحی داده های خود بر روی یک نمودار پراکندگی چند بعدی فکر کنید. سپس می توان به یک بردار ویژه منفرد را به عنوان ” جهت ” خاصی در نمودار پراکندگی داده ها در نظر گرفت. مقادیر ویژه نشان دهنده اندازه یا اهمیت هستند. مقادیر ویژه ی بالا تر با اهمیت بیشتر جهت ها همراه هستند.
درنهایت، ما فرض می کنیم که تغییر پذیری بیشتر در یک جهت خاص با توضیح رفتار متغیر وابسته مرتبط است. تغییر پذیری زیاد معمولاً نشان دهنده سیگنال است در حالی که تغییر پذیری کمی معمولاً نشان دهنده نویز است. بنابراین، تغییرپذیری بیشتر در یک جهت خاص، نشان دهنده چیزی با اهمیت است که ما می خواهیم کشف کنیم. ( برنامه ی PCA در سایت setosa.io یک روش بسیار عالی برای بازی با داده ها است و از این طریق می توانید خودتان را قانع کنید که چرا این کار منطقی است.)
بنابراین PCA روشی است که این موارد را به همراه می آورد:
- معیاری برای چگونگی ارتباط هر یک از متغیر ها با یکدیگر. (ماتریس کوواریانس.)
- جهتی که داده ها در آن پراکنده هستند. (بردارهای ویژه).
- اهمیت نسبی این جهت های مختلف. (مقادیر ویژه.)
PCA پیش بینی کننده های ما را ترکیب می کند و به ما اجازه می دهد بردار های ویژه ای را که نسبتاً بی اهمیت هستند، حذف کنیم.
بسط دهنده ای برای PCA وجود دارد؟
بله، بیش از آن چیزی که در فضای معقول این جا توانایی گفتن آن را داشته باشیم. موردی که بیش از همه مورد استفاده قرار می گیرد، رگرسیون مولفه های اصلی است که در آن ما Y تغییر نیافته را انتخاب می کنیم و آن را بر روی زیر مجموعه ای از Z* که حذف نکردیم، رگرسیون می کنیم. (این جایی است که مستقل بودن ستون های Z* به کار می آید؛ با رگرسیون کردن Y بر Z* ، می دانیم که استقلال لازم برای متغیر های مستقل لزوماً ارضا خواهد شد. با این حال، ما باید فرضیات دیگری را بررسی کنیم.)
گونه ی دیگر آن که معمولا دیده می شود، kernel PCA است.
نتیجه گیری
امیدوارم این مقاله مفید بوده باشد! برخی از منابع عمیق در مورد PCA را می توانید در سایت منبع بررسی کنید. بگذارید بدانیم شما چه فکر می کنید، به خصوص اگر پیشنهاداتی برای بهبود داشته باشید.
 مجله هوش مصنوعی شهاب
مجله هوش مصنوعی شهاب





سلام
ممنون از توضیحاتتون
بنده سوالی در این مورد داشتم
من اگر ماتریس ۱۰۰ در ۵ داشته باشم و بدین صورتی که فرمودین بخوام ارزشمندترین ویژگی هام رو پیدا کنم، از طریق متلب ماتریس مقادیر ویژه به صورت خودکار مرتب میشه و من قادر نیستم نهایتا بفهمم ترتیب مرتب شدن به چه صورت بوده و اولین مقدار ویژه برای کدوم ویژگی هست. برای این مورد آیا شما میدونین چیکار باید کرد؟
وقتی PCA را روی داده ها اعمال می کنید، در ماتریس خروجی، داده ها به فضایی می روند که در آنجا سطرهای ابتدایی، شامل بیشترین اطلاعات هستند. این سطرها با سطرهای ماتریس اولیه کاملا متفاوت هستند و ترکیبی از ویژگیهای ورودی هستند.
مقادیر ویژه بیانگر این هستند که هر مولفه اصلی چه درصدی از پراکندگی داده ها را پوشش می دهد و به ترتیب از بزرگ به کوچک و متناظر با مولفه های اصلی هستند.
خیلی ممنونم
شاهکار بود مقاله ی شما
ان شاالله که بیشتر بنویسید
ممنون از حسن نظر شما
سلام، خسته نباشید
ممنون از توضیحاتتون، من دانشجوی شیمی هستم و یکم توضیحات برام گنگ بود . امیدوارم بشه که یه مقاله با بیان ساده تر بنویسید که ما هم بتونیم استفاده کنیم.
سلام
پیشنهاد می کنیم این دو مطلب رو هم بررسی کنید.
https://shahaab-co.com/mag/edu/ml/dimensionality-reduction-tutorial/
https://shahaab-co.com/mag/videos/pca-step-by-step-tutorial/
سلام ، ممنون از مقاله ی جالب و مفیدتون
یه سوال داتشم از خدمت تون
به فرض ما سه مولفه RFM مربوط به تک تک مشتریان خودمون رو داریم (فرکانس خرید ، تازگی خرید و مبلغ ریالی خرید ) .
اگر بخوایم اون هارو به چند خوشه تقسیم بندی کنیم . آیا بجز استفاده از R یا پایتون راهی برای ان کار وجود داره ؟ ( چون فکر کنم نمودار Scatter تنها برای دو مولفه و نه بیشتر میتونه خوشه بندی انجام بده)
و سوال اصلی اینکه یه ویژوال Clustering برای power bi تحت نمودار Scatter وجود داره که میتونه بیش از دو مولفه رو خوشه بندی کنه . در بخش تنظیماتش هم گزینه Apply PCA وجود داره . با توجه به اینکه ما بر اساس ۳ مولفه RFM قصد داریم خوشه بندی رو انجام بدیم ، آیا اعمال کرد PCA کیفیت خوشه بندی رو بهتر میکنه ؟
سلام
سوالتون یک مقدار ابهام داره.
PCA یک روش برای کاهش ابعاد ویژگیهاست و ذاتا برای خوشه بندی نیست. اگر تنها سه ویژگی دارید نیازی به استفاده از PCA نیست. برای خوشه بندی بهتر است از KMeans یا SOM استفاده کنید.
ضمنا برای پیاده سازی روشهای یادگیری ماشین، ساده ترینش همان پایتون و R هست. بعد می توانید سراغ متلب و ++C هم بروید.
سلام
وقت بخیر
من یک تعداد داده دارم ماتریس کوواریانس داده ها هم ایجاد شده اما چون تعداد داده ها خیلی زیاد هس و برای محاسبه ی معکوسش در ابعاد بالا با چالش مواجه میشم
هدفم کم کردن ابعاد ماتریس برای راحتی محاسبه ی معکوس ماتریس کوواریانس هس
چجوری میتونم از این روش استفاده کنم؟
منظورم توی متلب هس
اگه منو راهنمایی کنین ممنون میشم
سلام
میتوانید از روش های کاهش بعد مثل PCA و IDA استفاده کنید. با کمی جست و جو در وب می توانید دستوررات متلب را بیابید.
سلام وقتتون بخیر میشه منابعی ک ازشون استفاده کردین رو هم بزارین؟؟
سلام
منابع در انتهای مطلب ذکر شدن
سلام ممنون از مطالب مفیدتون. سوالم اینه در کاهش ویژگی برای مثلا من ده متغیر دارم با روش pca بعد از اجرای دستور جداولی میآورد ک تعداد مولفه های انتخاب شده را با شماره یک تا… مشخص کرده خب من چطور باید بفهمم ک این شماره ها مربوط ب کدوم متغیر هاست ک انتخاب شده؟
ترجمه بسیار ضعیف است. اما بهر حال ممنون.
بابت مشکلات ترجمه عذرخواهی میکنیم و برای بهبود ترجمه های بعدی تمام تلاشمون رو میکنیم
از آماده سازی و ترجمه این متن که مطالب سعی شده با دقت بیان شود و قابل درک باشد و نیز معرفی رفرنس و سایت برای مطالعه و فهم بیشتر مطالب توضیح داده شده خیلی سپاسگزارم.