در این سری از آموزش پردازش تصویر با MATLAB ، قصد داریم با استفاده از فرآیند مات زدایی تصویر ( Image Deblurring ) و تبدیل هاف ( Hough Transform ) ، نگاهی به پیش پردازش تصویر و تشخیص اشیاء خاص در تصویر داشته باشیم.

هدف از مات زدایی یک تصویر که با استفاده از تابع نقطه گستر (PSF) انجام می شود، حذف اعوجاج از تصویر مات شده است. الگوریتم های رفع ماتی تصویر در جعبه ابزار پردازش تصویر شامل دکانولوشن فیلتر وینر ( Wiener )، و فیلتر منظم ( regularised ) ، دکانولوشن کور ( blind )، لوسی-ریچاردسون ( Lucy-Richardson ) ، و همچنین تبدیل بین PSF و OTF است. این توابع در رفع ماتی ناشی از اپتیک خارج از فوکوس، حرکت دوربین یا سوژه در حین ثبت تصویر، شرایط جوی نامناسب، زمان نوردهی محدود و عوامل دیگر مؤثر هستند.

تابع deconvwnr ، تصویر را با استفاده از فیلتر Wiener مات زدایی می کند، در حالی که تابع deconvreg ، عملیات مات زدایی را با یک فیلتر منظم انجام می دهد. تابع deconvlucy یک الگوریتم لوسی-ریچاردسون تسریع شده را پیاده سازی می کند و تابع deconvblind الگوریتم دکانولوشن کور را پیاده سازی می کند که بدون اطلاع از PSF، عملیات مات زدایی را انجام می دهد. ما در این مقاله در مورد چگونگی رفع مات شدگی یک تصویر با استفاده از فیلتر های وینر و منظم صحبت می کنیم.

مات زدایی با استفاده از فیلتر Wiener

هنگامی که ویژگی های فرکانسی تصویر و نویز جمع شونده تا حدودی شناخته شده و معلوم باشند، می توان به طور موثری از دکانولوشن وینر استفاده کرد. در صورت عدم وجود نویز، فیلتر وینر به یک فیلتر معکوس ایده آل تبدیل می یابد.

تابع deconvwnr تصویر I را با استفاده از الگوریتم فیلتر وینر دکانوالو می کند و تصویر J مات زدایی شده را به صورت زیر برمی گرداند:

J = deconvwnr(I,PSF,NSR)

که در آن تصویر I می‌تواند یک آرایه N بعدی باشد و PSF تابع نقطه گستر است که تصویر I با آن کانوالو شده، و NSR نسبت توان نویز به سیگنال برای نویز جمع شونده است. NSR می تواند یک آرایه اسکالر یا یک آرایه دامنه طیفی ( spectral-domain ) هم اندازه با تصویر I باشد. NSR=0 معادل ایجاد یک فیلتر معکوس ایده آل است. تصویر I می‌تواند از کلاس uint8، uint16، int16، single یا double باشد. سایر ورودی ها باید از کلاس double باشند. همچنین تصویر J دارای کلاس مشابه با تصویر I است.

مراحل زیر به ترتیب برای فراخوانی Image_2.tif””، مات کردن آن ، اضافه کردن نویز به آن و سپس بازیابی تصویر با استفاده از فیلتر وینر انجام می گیرد.

برای فراخوانی تصویر(Image_2.tif) و نمایش آن در محیط MATLAB از دستورات زیر استفاده می کنیم:

>> I=im2double(imread(‘Image_2.tif’));
>>imshow(I)

تصویر فراخوانی شده در متلب — شکل ۱: فراخوانی تصویر در محیط MATLAB

دستور h=fspecial(‘motion’, len, theta) ، فیلتری را برای تقریب حرکت خطی دوربین به تعداد len پیکسل و با زاویه theta درجه در خلاف جهت عقربه های ساعت برمی گرداند. فیلتر برای حرکات افقی و عمودی به یک بردار تبدیل می شود. مقدار پیش فرض len برابر ۹ و مقدار theta برابر صفر است که بیانگر حرکت افقی با ۹ پیکسل است. B=imfilter(A,h) آرایه چند بعدی A را با فیلتر چند بعدی h فیلتر می کند. آرایه A می تواند آرایه عددی از هر کلاس و بعدی باشد. خروجی B اندازه و کلاس مشابه A دارد. مطابق دستورات زیر :

>> LEN=21;
>> THETA=11;
>> PSF=fspecial(‘motion’,LEN,THETA);
>> blurred=imfilter(I,PSF,’conv’,’circular’);
>>figure,imshow(blurred)

تصویر خروجی فیلتر چند بعدی — شکل ۲: تصویر پس از فیلتر کردن با فیلتر چند بعدی

دستور J=imnoise (I,’gaussian’,M,V) نویز سفید گاوسی با میانگین M و واریانس V را به تصویر I اضافه می کند:

>>noise_mean=0;
>>noise_var=0.002;
>>blurred_noise=imnoise(blurred,’gaussian’,
noise_mean,noise_var);
>>figure, imshow(blurred_noise)

عکس با نویز سفید گاوسی — شکل ۳: تصویر ایجاد شده پس از اضافه کردن نویز سفید گاوسی

همانطور که اشاره شد، J=deconvwnr (I,PSF,NSR) تصویر I را با استفاده از الگوریتم فیلتر وینر بازمی گرداند و تصویر مات زدایی شده J را برمی گرداند. دستورات زیر با استفاده از NSR صفر یک تصویر بدون ماتی ایجاد می کنند:

>>estimated_nsr=0;
>> wnr2=deconvwnr(blurred_noise,PSF,estimated_nsr);
>>figure,imshow(wnr2)

تصویر مات زدایی شده با NSR — شکل ۴: تصویر مات زدایی شده با استفاده از NSR صفر

دستورات زیر با استفاده از NSR محاسبه شده از تصویر، یک تصویر مات زدایی شده ایجاد می کنند:

>>estimated_nsr=noise_var/var(I(:));
>> wnr3=deconvwnr(blurred_noise,PSF,estimated_nsr);
>>figure,imshow(wnr3)

شکل ۵ تصویر بازیابی شده از تصویر مات و نویزی را با استفاده از NSR تخمین زده شده از تصویر نشان می دهد.

مات زدایی با فیلتر منظم

هنگامی که اطلاعات محدودی در مورد نویز جمع شونده در اختیار باشد، می توان از یک فیلتر منظم استفاده کرد.

دستور J=deconvreg(I, PSF) تصویر I را با استفاده از الگوریتم فیلتر منظم دکانوالو می کند و تصویر مات زدایی شده J را برمی گرداند. فرض بر این است که تصویر I با دکانولوشن یک تصویر حقیقی با یک تابع نقطه گستر و احتمالاً با اضافه کردن نویز ایجاد شده است. الگوریتم بهینه سازی مقید به معنای حداقل مربعات خطا بین تصاویر تخمین زده شده و تصویر حقیقی است که نیاز به حفظ وضوح تصویر دارد. همچنین تصویر I می تواند یک آرایه N بعدی باشد.

تغییرات تابع deconverg در زیر آورده شده است:

J = deconvreg(I, PSF, NOISEPOWER)

که در آن NOISEPOWER توان نویز جمع شونده است و مقدار پیش فرض آن ۰ است.

J = deconvreg(I, PSF, NOISEPOWER, LRANGE)

که در آن LRANGE برداری است که محدوده ای را مشخص می کند که در آن جستجو برای راه حل بهینه انجام می شود.

الگوریتم ، یک ضریب لاگرانژ بهینه LAGRA را در محدوده LRANGE پیدا می کند. اگر LRANGE یک اسکالر باشد، الگوریتم فرض می‌کند که LAGRA مشخص شده و برابر با LRANGE است. سپس مقدار NP نادیده گرفته می شود. محدوده پیش فرض آن بین [۱e-9 and 1e9] است.

J = deconvreg(I, PSF, NOISEPOWER, LRANGE, REGOP)

که در آن REGOP عملگر منظم سازی برای محدود کردن دکانولوشن است. عملگر منظم سازی پیش فرض عملگر لاپلاسین است تا وضوح تصویر را حفظ کند. ابعاد آرایه REGOP نباید از ابعاد تصویر بیشتر باشد. هر ابعاد غیر تک عضوی باید با ابعاد غیر تک عضو PSF مطابقت داشته باشد.

[J, LAGRA] = deconvreg(I, PSF,…) مقدار ضریب لاگرانژ LAGRA را علاوه بر تصویر J بازیابی شده خروجی می دهد.

به طور خلاصه ، تابع deconverg از چند آرگومان اختیاری پشتیبانی می گند. با استفاده از این آرگومان ها می توانید مقدار توان نویز، محدوده ای را که deconverg باید در آن تکرار شود، و عملگر منظم سازی را برای مقید کردن دکانولوشن مشخص کنید.

تصویر I می‌تواند از کلاس uint8، uint16، int16، single یا double باشد. ورودی های دیگر باید از کلاس double باشند. تصویر J و تصویر I از یک کلاس مشابه است.

مثال زیر یک تصویر مات شده را با کانولوشن یک فیلتر گاوسی PSF با یک تصویر (با استفاده از imfilter) شبیه‌سازی می کند:

فراخوانی یک تصویر را در متلب:

>> I=imread(‘image_2.tif’);
>>figure,imshow(I)

تصویر ورودی در متلب — شکل ۶: تصویر فراخوانی شده در متلب

ساخت PSF و تصویر مات و سپس افزودن نویز به آن:

>> PSF = fspecial(‘gaussian’,۱۱,۵);
>> Blurred = imfilter(I,PSF,’conv’);
>> V=0.03;
>>Blurred_Noise=imnoise(Blurred,’gaussian’,۰,V);
>>figure,imshow(Blurred_Noise)

تصویر محو شده و نویزی — شکل ۷: تصویر مات و نویزی

توجه داشته باشید که نویز جمع شونده در تصویر با افزودن نویز گاوسی با واریانس V به تصویر مات شده (با استفاده از imnoise) شبیه سازی می شود. شکل ۷ تصویر مات و نویزی را نشان می دهد.

تصویر با استفاده از تابع deconverg مات زدایی می شود و PSF مورد استفاده برای ایجاد تاری و همچنین توان نویز(NP) را مشخص می کند:

>> NP=V*prod(size(I));
>> [reg1 LAGRA] = deconvreg(Blurred_Noise,PSF,NP);
>>figure, imshow(reg1)

شکل ۸ تصویر بازیابی شده را نشان می دهد.

تبدیل هاف (Hough transform)

تبدیل هاف برای شناسایی خطوط و منحنی ها در یک تصویر طراحی شده است. با استفاده از تبدیل هاف، می توانید پاره خط ها و نقاط انتهایی را پیدا کنید، زاویه ها را اندازه گیری کنید، دایره ها را بر حسب اندازه پیدا کنید، و اجسام گرد را در یک تصویر شناسایی و اندازه‌گیری کنید.

در مثال تبدیل هاف زیر، یک تصویر را فراخوانی می کنیم، دایره ها یا اشیاء گرد و دایره شکل را بطور خودکار تشخیص داده و دایره های شناسایی شده را رسم می کنیم.

فراخوانی تصویر و نمایش آن: این مثال از تصویری با دایره های رنگی استفاده می کند:

>> I=imread(‘Image_3.png’);
>>figure, imshow(I)

تصویر نمایش داده شده از دایره ها — شکل ۹: تصویر دایره هایی با رنگ های مختلف فراخوانی شده و نمایش داده می شود

تعیین محدوده شعاع برای جستجوی دایره ها: یک راه سریع برای یافتن محدوده شعاع مناسب استفاده از ابزار تعاملی imdistline است که تخمینی از شعاع اجسام مختلف ارائه می دهد.

h = imdistline یک ابزار Distance در محور فعلی ایجاد می کند. ابزار Distance یا فاصله یک خط قابل تغییر اندازه است که روی یک محور قرار گرفته و فاصله بین دو نقطه انتهایی خط را اندازه می گیرد و این فاصله را در یک برچسب متنی که روی خط قرار گرفته است نشان می دهد. این ابزار فاصله را در واحدهای داده تعیین شده توسط ویژگی های XData و YData مشخص می کند که به طور پیش فرض بر حسب پیکسل است.

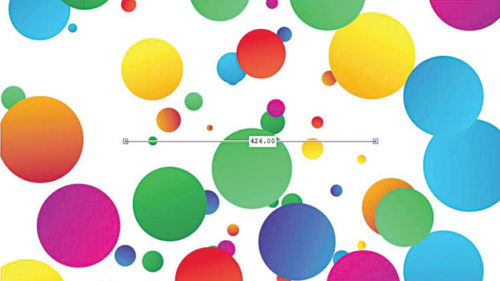
استفاده از ابزار تعاملی imdistline در متلب — شکل ۱۰: استفاده ابزار تعاملی imdistline در متلب

اگر از دستور زیر استفاده می شد، شکل ۹ به شکل نشان داده شده در شکل ۱۰ تغییر می کرد:

>>d = imdistline

خط را می توان برای به دست آوردن اندازه دایره های مختلف رسم کرد.

به طور خلاصه، دستور imdistline یک ابزار قابل ترسیم ایجاد می کند که می تواند حرکت کند تا روی یک دایره قرار گیرد و از اعداد خروجی آن می توان برای تخمین تقریبی شعاع استفاده کرد.

برای حذف ابزار imdistline، از تابع استفاده زیر کنید:

>>delete(d);

تصویر تعدادی دایره رنگی — شکل ۱۱: تصویر با تعدادی دایره

تصویر نشان داده شده در شکل ۱۱ را در نظر بگیرید. هدف یافتن تعداد دایره ها در شکل است.

کاملاً بدیهی است که دایره های زیادی با رنگ های مختلف با کنتراست های متفاوت نسبت به پس زمینه وجود دارد. دایره های آبی و قرمز نسبت به پس زمینه کنتراست قوی تری دارند، در حالی که دایره های سفید و زرد ضعیف ترین کنتراست را نسبت به پس زمینه دارند.

یافتن اجسامی را که روشن تر و تیره تر از پس زمینه هستند: برای این کار باید این تصویر RGB را به مقیاس خاکستری تبدیل کنیم:

>> RGB=imread(‘Image_4.png’);
>>gray_image=rgb2gray(RGB);
>>figure, imshow(gray_image)

تصویر خاکستری شده دایره های رنگی — شکل ۱۲: تصویر RGB در شکل ۱۱ به تصویر خاکستری تبدیل شده است

شکل ۱۲ تصویر خاکستری را نشان می دهد

تابع centers=imfindcircles (A,radius) دایره هایی را در تصویر A پیدا می کند که شعاع آن ها تقریباً برابر با شعاع radius است. خروجی آن، یک ماتریس دو ستونی است که شامل مختصات(x,y) مراکز دایره های موجود در تصویر است.

دستور [centers,radii] = imfindcircles (A,radiusRange) دایره هایی با شعاع در محدوده مشخص شده توسط radiusRange را پیدا می کند. آرگومان خروجی radii ، شامل شعاع های تخمینی مربوط به مرکز هر دایره در centers است.

به طور پیش فرض، imfindcircles اشیاء دایره ای را پیدا می کند که روشن تر از پس زمینه هستند. در مثال ما، اجازه دهید برای جستجوی دایره های تاریک، پارامتر ObjectPolarity را روی Dark قرار دهیم:

>> [centers,radii]=imfindcircles(RGB,[40 60],’ObjectPolarity’,’Dark’)

نتیجه دستورات بالا به صورت زیر است:

centers = 384.2814 204.1827
radii = 50.1646

همانطور که ملاحظه می کنید، فقط یک دایره شناسایی می شود. زیرا imfindcircles یک آشکارساز دایره است و مشابه اکثر آشکارسازها، imfindcircles یک آستانه تشخیص داخلی دارد که حساسیت آن را تعیین می کند. imfindcircles دارای یک پارامتر “حساسیت” است که می توان از آن برای کنترل این آستانه داخلی و در نتیجه حساسیت الگوریتم استفاده کرد. مقدار حساسیت بالاتر آستانه ، تشخیص کمتری را تعیین می کند و منجر به شناسایی دایره های بیشتر می شود. این شبیه به کنترل حساسیت در آشکارسازهای تشخیص حرکت است که در سیستم های امنیتی منازل استفاده می شود.

به طور پیش فرض حساسیت که عددی بین ۰ و ۱ است روی ۰٫۸۵ تنظیم شده است. با افزایش حساسیت به ۰٫۹ به صورت زیر:

>> [centers,radii]=imfindcircles(RGB,[40 60],’ObjectPolarity’,’Dark’,’Sensitivity’,۰٫۹)

نتایج زیر را خواهید داشت:

centers =
۳۸۴٫۲۰۰۲ ۲۰۴٫۰۱۳۸
۲۴۸٫۶۱۲۷ ۲۰۱٫۳۴۱۶
۱۹۸٫۲۸۲۵ ۷۳٫۵۶۱۸
۴۴۲٫۸۰۹۱ ۷۷٫۹۰۶۰
radii =
۵۰٫۱۶۴۶
۵۰٫۲۵۷۲
۵۰٫۲۹۵۱
۴۹٫۷۸۲۷

با افزایش حساسیت به ۰٫۹، تابع imfindcircles چهار دایره پیدا کرد. ‘centers’ شامل مکان های مرکزی دایره ها و ‘radii’ شامل شعاع تخمینی این دایره ها است.

۷٫ از تابع viscircles می توان برای ترسم دایره روی تصویر استفاده کرد. از متغیر های خروجی ‘centers’ و ‘radii’ تابع imfindcircles می توان مستقیماً در تابع viscircles استفاده کرد.

>>imshow(RGB)
>> h=viscircles(centers,radii)

ترسیم اشکال با تابع viscircles — شکل ۱۳: ترسیم دایره ها با استفاده از تابع viscircles

همانطور که در شکل ۱۳ ملاحظه می کنید، به نظر می رسد که مراکز دایره ها به درستی قرار گرفته اند و به نظر می رسد شعاع متناظر آن ها به خوبی با دایره های واقعی مطابقت دارد. با این حال، تعداد زیادی از دایره ها پیدا نشدند. اجازه دهید “حساسیت” را به ۰٫۹۲۸ افزایش دهیم:

>> [centers,radii]=imfindcircles(RGB,
[۴۰ ۶۰],’ObjectPolarity’,’Dark’,’Sensitivity’,۰٫۹۸)

centers =
۳۸۴٫۲۱۹۳ ۲۰۴٫۴۷۷۶
۲۴۸٫۸۴۴۶ ۲۰۱٫۴۹۳۰
۱۹۷٫۷۰۲۷ ۷۳٫۵۱۴۹
۴۴۲٫۹۹۹۸ ۷۸٫۳۶۷۴
۷۶٫۷۲۱۸ ۷۶٫۵۱۶۲
radii =
۵۰٫۱۶۴۶
۵۰٫۲۵۷۲
۵۰٫۲۹۵۱
۴۹٫۷۸۲۷
۵۰٫۴۰۳۹

اکنون می توانیم پنج دایره را شناسایی کنیم. از این رو، با افزایش مقدار حساسیت می توانید دایره های بیشتری را شناسایی کنید. اجازه دهید دوباره این دایره ها را روی تصویر رسم کنیم:

>>delete(h); % Delete previously drawn circles
>>h = viscircles(centers,radii);

همانطور که مشاهده می کنید، تابع imfindcircles دایره های زرد و سفید را در تصویر پیدا نمی کند. دایره های زرد و سفید روشن تر از پس زمینه هستند. در واقع، به نظر می رسد که این ها شدت روشنایی های بسیار مشابهی با پس زمینه دارند. برای تأیید این موضوع، اجازه دهید نسخه خاکستری تصویر اصلی را دوباره ببینیم. شکل ۱۵ تصویر خاکستری را نشان می دهد.

>>figure, imshow(gray_image)

تصویر خاکستری شده دایره ها — شکل ۱۴: نسخه خاکستری تصویر در شکل ۱۴

برای تشخیص اشیا روشن تر از پس زمینه، ObjectPolarity را به Bright تغییر دهید:

>> [centers,radii]=imfindcircles(RGB,[40 60],’ObjectPolarity’,’Bright’,’Sensitivity’,۰٫۹۸)

centers =
۳۲۳٫۲۸۰۶ ۷۵٫۹۶۴۴
۱۲۲٫۳۴۲۱ ۲۰۵٫۱۵۰۴
radii =
۴۹٫۷۶۵۴
۵۰٫۱۵۷۴

می توان با تغییر پارامتر ‘Color’ در دایره ها، دایره های روشن را با رنگی متفاوت ترسیم کرد:

>>imshow(RGB)
>>hBright=viscircles(centers,radii,’Color’,’b’);

تصویر ترسیم شده دایره ها — شکل ۱۶: دایره های روشن با رنگی متفاوت ترسیم شده اند

پارامتر دیگری در تابع imfindcircles وجود دارد، یعنی EdgeThreshold، که مقدار گرادیان در یک پیکسل را قبل از اینکه یک پیکسل لبه در نظر گرفته شود و در محاسبات لحاظ شود ، کنترل می کند. یک مقدار زیاد (نزدیک به ۱) برای این پارامتر اجازه می دهد که فقط لبه های قوی (مقادیر گرادیان بالاتر) را لحاظ گند، در حالی که مقدار پایین (نزدیک به ۰) لبه های ضعیف تر (مقادیر گرادیان پایین) را در بر می گیرد. بنابراین، با کاهش مقدار پارامتر EdgeThreshold، شانس تشخیص دایره ها بیشتر می شود. با این حال، احتمال تشخیص دایره های کاذب نیز افزایش می یابد. از این رو، بین تعداد دایره های واقعی که می توان پیدا کرد (نرخ تشخیص) و تعداد دایره های نادرستی که با آن ها یافت می‌شوند (نرخ هشدار نادرست) یک مصالحه یا تعادل وجود دارد.

دستورات زیر هم اجسام روشن و هم تاریک را شناسایی کرده و دور آن ها دایره رسم می کند:

>>[centersBright,radiiBright,metricBright]=imfindcircles(RGB,[4060], ‘ObjectPolarity’,’bright’,’Sensitivity’,۰٫۹,’EdgeThreshold’,۰٫۲);
>>imshow(RGB);
>> h=viscircles(centers,radii);
>>hBright=viscircles(centersBright,radiiBright,’Color’,’b’);