مقدمه
در آموزش قبلی یادگیری ماشین ، ما در مورد SVM ( ماشین بردار پشتیبان ) در یادگیری ماشین بحث کرده ایم. اکنون قصد داریم شرح مفصلی از توابع کرنل SVM و کرنل های مختلف و نمونه هابی از جمله خطی ، غیرخطی ، چند جمله ای ، کرنل گاوسی ، تابع پایه شعاعی ( RBF ) ، سیگموئید و غیره را برای شما ارائه دهیم.

توابع کرنل SVM
الگوریتم های SVM از مجموعه ای از توابع ریاضی که به عنوان کرنل تعریف می شوند، استفاده می کنند. وظیفه کرنل این است که داده ها را به عنوان ورودی گرفته و آن ها را به شکل مورد نیاز تبدیل کند. الگوریتم های مختلف SVM ، از انواع مختلف توابع کرنل استفاده می کنند. این توابع می توانند انواع متفاوتی داشته باشند. به عنوان مثال خطی ، غیرخطی ، چند جمله ای ، تابع پایه شعاعی (RBF) و سیگموئید.
توابع کرنل ، برای داده های ترتیبی ، نمودار ها ، متن ها ، تصاویر و همچنین بردار ها معرفی می شوند. پرکاربردترین نوع تابع کرنل، RBF است. زیرا دارای پاسخ محلی و متناهی در کل بازه محور x است.
توابع کرنل ، ضرب داخلی بین دو نقطه در یک فضای ویژگی مناسب را برمی گردانند. بنابراین ، با هزینه محاسباتی کم، حتی در فضاهای با ابعاد بالا، مفهومی از شباهت را تعریف می کنند.
قواعد کرنل
تعریف کرنل یا یک تابع پنجره به شرح زیر است:
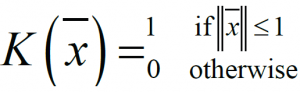
مقدار این تابع، در داخل یک شکل بسته به دامنه ۱ و مرکز مبدا مختصات برابر ۱ و در غیر این صورت ۰ است. همانطور که در شکل زیر نشان داده شده است:
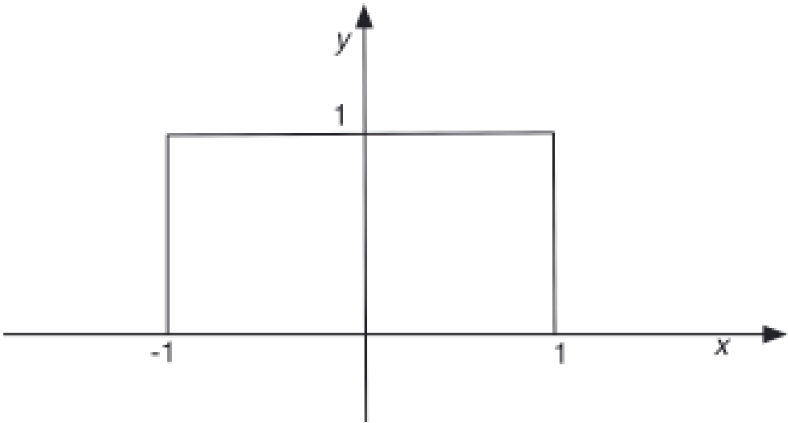
برای xi ثابت، در داخل شکل بسته با دامنه h و مرکز xi ، تابع برابر است با K (z – xi / h) = 1 و در غیر این صورت ۰ می باشد. همانطور که در شکل زیر نشان داده شده است :
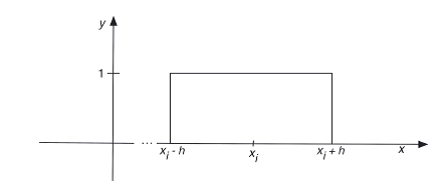
بنابراین ، با انتخاب آرگومان (.)K ، پنجره را حرکت داده اید تا با دامنه h در مرکز xi قرار گیرد.
نمونه هایی از کرنل های SVM
بیاید برخی از کرنل های رایج مورد استفاده در SVM ها و کاربرد های آن ها را مشاهده کنیم :
۱- کرنل چند جمله ای
این کرنل در پردازش تصویر پرکاربرد است. معادله آن به صورت زیر است :
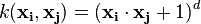
که در آن d درجه چند جمله ای است.
۲- کرنل گاوسی
این یک کرنل برای اهداف عمومی است. و هنگامی که هیچ دانش پیشینی در مورد داده ها وجود ندارد استفاده می شود. معادله آن به صورت زیر است :
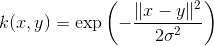
۳- تابع پایه شعاعی گاوسی ( RBF )
این کرنلی برای اهداف عمومی کلربرد دارد. و هنگامی که هیچ دانش پیشینی در مورد داده ها وجود نداشته باشد، مورد استفاده قرار می گیرد. معادله آن به صورت زیر است :
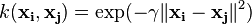
و برای

گاهی اوقات با استفاده از پارامتر زیر استفاده می شود :
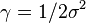
۴- کرنل RBF لاپلاس
این هم یک کرنل برای اهداف عمومی است. و هنگامی که هیچ دانش پیشینی در مورد داده ها وجود ندارد استفاده می شود. معادله آن به صورت زیر است :
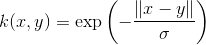
۵- کرنل تانژانت هیپربولیک ( tanh )
می توانیم از آن در شبکه های عصبی استفاده کنیم. معادله مربوط به آن عبارت است از :
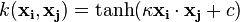
در برخی موارد ( نه همیشه ) k > 0 و c < 0.
۶- کرنل سیگموئید
می توان این کرنل را در شبکه های عصبی مورد استفاده قرار داد. معادله مربوط به آن عبارت است از :
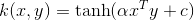
۷- کرنل تابع بِسِل ( Bessel ) از نوع اول
ما می توانیم از آن برای حذف مقطع عرضی در توابع ریاضی استفاده کنیم. معادله آن عبارت است از :
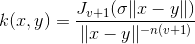
که J تابع بسل از نوع اول است.
۸- کرنل پایه شعاعی ANOVA
ما می توانیم از آن در مسائل رگرسیون استفاده کنیم. معادله مربوط به آن عبارت است از :
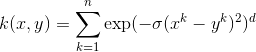
۹- کرنل spline خطی بصورت یک بعدی
این کرنل، هنگام کار با بردارهای بزرگ داده پراکنده ، کاربرد زیادی دارد. این کرنل اغلب در دسته بندی متن مورد استفاده قرار می گیرد. کرنل spline همچنین در مسائل رگرسیون عملکرد خوبی دارد. معادله آن عبارت است از :
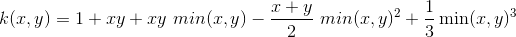
اگر در مورد توابع کرنل SVM سوالی دارید ، در صورت تمایل با ما در میان بگذارید. ما از این که پاسخگوی سوالات شما باشیم خوشحال خواهیم شد.
 مجله هوش مصنوعی شهاب
مجله هوش مصنوعی شهاب




