شبکه های عصبی : از صفر تا صد

درباره مهمترین پارامترهای شبکه های عصبی اطلاعات کسب کنید!

در طول این مقاله مباحث زیر شرح داده می شود:

• نظریه بهینه سازی : گرادیان نزولی و تغییرات آن
• نرخ یادگیری و اندازه دسته
• توابع ضرر و فعال سازی
• مقداردهی اولیه وزن

نظریه بهینه سازی: گرادیان نزولی  و تغییرات آن

اگر توضیح مفصلی از گرادیان نزولی بخواهید، توصیه می کنم این مقاله را که در آن ریاضیاتی که شبکه های عصبی بر اساس آن پایه گذاری شده را به صورت عمیق توضیح داده، بررسی کنید.

به طور خلاصه، گرادیان نزولی خطای هر نمونه در مجموعه آموزش را محاسبه می کند و سپس وزن ها را در جهتی که شیب نشان می دهد، به روز می کند.

به عبارت دیگر، برای هر دوره ( Epoch )، ما باید:

• هر پیش بینی ای را محاسبه کنیم ( پیش روی ( Forward Pass ) ).
• هر خطایی را محاسبه کنیم.
• خطا ها را به عقب انتشار دهید (پس انتشار خطا) تا اهمیت هر وزن در این خطا را ارزیابی کنیم.
• و در آخر، وزن را به تبع آن به روز کنیم.

بیایید تصور کنیم که ما اطلاعات زیر را داریم:

• مجموعه داده ای از ۱۰۰۰۰۰ نمونه،
• هر پیش روی ۲ms طول بکشد.
• هر محاسبه خطا ۱ms طول بکشد.
• هر پس انتشار ۳ms طول بکشد.

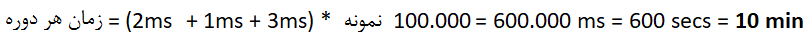
ممکن است یک شبکه عصبی معمول به همگرایی مناسب صد ها ، یا حتی هزاران دوره نیاز داشته باشد. فرض کنیم که ما به ۱۰۰ دوره نیاز داریم، که تعداد کمی است.

آموزش شبکه عصبی ما چقدر طول خواهد کشید؟

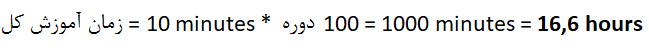
این زمان خیلی زیادی است. و خوش بینانه فرض کردیم که فقط ۱۰۰۰۰۰ نمونه داشتیم. به عنوان مثال تصویر خالص از ۱٫۲ میلیون تصویر تشکیل شده است و هر دوره ۲ ساعت یا به عبارت دیگر ۸٫۳ روز طول می کشد. بیش از یک هفته طول می کشد تا رفتار یک شبکه را ببینید.

یکی از راه ها برای کاهش چشمگیر زمان مورد نیاز برای آموزش شبکه عصبی استفاده از یک نمونه واحد است که هر بار که بخواهیم وزن ها را به روز کنیم، به طور تصادفی انتخاب می شود.

این روش گرادیان نزولی تصادفی ( Stochastic Gradient Descent ) نامیده می شود. با استفاده از گرادیان نزولی تصادفی ، ما فقط باید پیش بینی ها، خطا ها و  پس انتشار یک نمونه را برای به روز رسانی وزن ها، محاسبه کنیم.

این باعث کاهش کل زمان آموزش به صورت زیر می شود:

این یک پیشرفت بزرگ است. اما این روش یک ضرر بسیار مهم دارد.

از بین این دو مسیر، کدام یک را فکر می کنید که از گرادیان نزولی دنبال کرده است؟ و کدام یک از گرادیان نزولی تصادفی ؟

مسیر قرمز مسیری است که از گرادیان نزولی دنبال می کند. این روش گرادیان (مسیر نزولی) را با استفاده از تمام نمونه های مجموعه داده محاسبه می کند و به روز رسانی استواری را همیشه در جهت کاهش خطا فراهم می کند.

مسیر بنفش مسیری است که گرادیان نزولی تصادفی پیروی می کند. چه اتفاقی افتاده است؟ هر به به روزرسانی وزن برای به حداقل رساندن خطا با در نظر گرفتن تنها یک نمونه انجام شده است، بنابراین آنچه که ما به حداقل می رسانیم خطا برای آن نمونه خاص است.

به همین دلیل است که رفتار پر هرج و مرج تری داشته و همگرایی بیشتر طول می کشد، اگرچه در عوض، خیلی سریع تر اجرا می شود، بنابراین در زمانی که گرادیان نزولی باید دوره ای را اجرا کند، گرادیان نزولی تصادفی می تواند هزاران دوره را اجرا کند.

به نظر می رسد بهترین گزینه این است که تعادل با هر دو روش برقرار شود. اگر به عکس قبلی نگاهی بیندازیم، بهترین مسیر خط سبز است.

برای محاسبه این مسیر، بگذارید روش های مورد بحث تا کنون را مرور کنیم:

• روشی که پیش بینی ها و خطاهای کلیه عناصر مجموعه آموزشی ما را محاسبه می کند: گرادیان نزولی
• روشی که پیش بینی ها و خطاهای مربوط به یک عنصر انتخاب شده تصادفی از مجموعه آموزشی ما را محاسبه می کند: گرادیان نزولی تصادفی

چه می شود اگر به جای یک عنصر، K عنصر را انتخاب کنیم؟ در این صورت:

• ما ثبات الگوریتم را افزایش می دهیم زیرا فقط به یک عنصر نه، بلکه به K عنصر نگاه می کنیم (یعنی ما تغییرات ناگهانی و بی نظم جهت را که خط بنفش دارد، کاهش دادیم).
• ما زمان اجرای مربوط به گرادیان نزولی سنتی را کاهش دادیم، زیرا از تعداد N نمونه که مجموعه آموزشی ما دارد، به K نمونه رفتیم، جایی که K << N

این روش با عنوان گرادیان نزولی تصادفی دسته کوچک (Mini-batch Stochastic Gradient Descent ) شناخته می شود و معروف ترین روش در عمل است.

K معمولاً به عنوان توان ۲ انتخاب می شود، زیرا این امر به شما امکان می دهد از برخی بهینه سازی هایی که GPU برای این موارد دارند، استفاده کنید. یک K معمولی ممکن است K = 32 باشد، اما در پایان، توسط حافظه GPU محدود می شود.

هرچه K کم تر باشد، بیشتر به گرادیان نزولی تصادفی خالص شباهت می یابد، و دوره های بیشتری برای همگرایی نیاز خواهند داشت، اگرچه این نیز صحت دارد که آن ها را سریع تر محاسبه می کند.

از طرف دیگر، هرچه K بیشتر باشد، بیشتر شبیه گرادیان نزولی خالص خواهد بود و برای محاسبه هر دوره، مشکل بیشتری خواهد داشت، اما برای همگرایی به دوره های کمتری نیاز دارد.

نرخ یادگیری و اندازه دسته

نرخ یادگیری و اندازه دسته دو پارامتری هستند که به طور مستقیم با الگوریتم گرادیان نزولی در ارتباط هستند.

نرخ یادگیری

همانطور که ممکن است بدانید، (یا اگر نمی دانید، اینجا می توانید بررسی کنید) راه به روزرسانی وزن های عصبی از طریق این فرمول ها است:

آنچه در (∂E_{total /} ∂W_n) ضرب می شود η که نرخ یادگیری نامیده می شود. نرخ یادگیری بیانگر اهمیتی است که برای به روزرسانی هر وزن به خطا اطلاق می کنیم. این یعنی تغییرات در وزن ها چقدر سریع یا ناگهانی است.

بنابراین، یک η بسیار بالا، در مراحل بزرگی از یک تکرار به دیگری ، باعث تغییر ناگهانی در وزن خواهد شد، که می تواند باعث پریدن از حداقل شود.

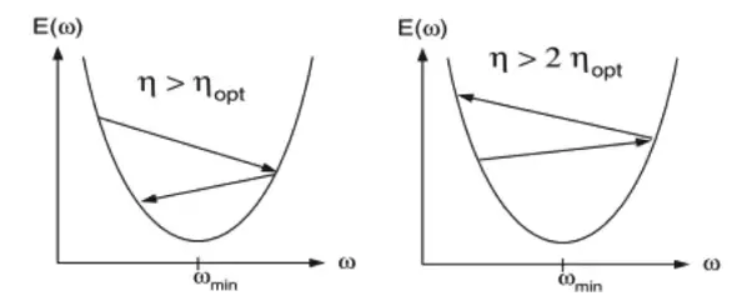
امکان دیگر ایجاد یک η بسیار پایین است، که باعث می شود شبکه ما برای رسیدن به حداقل قابل قبول، به دوره های خیلی زیادی احتیاج داشته باشد. همچنین، ریسک به دام افتادن در بدترین حداقل نسبت به بهترینی که می توانیم با η بالاتر بدست آوریم را دارد.

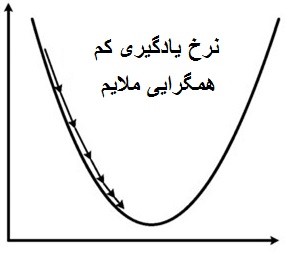
بیایید در مورد حداقل ها صحبت کنیم : آنچه معمولاً با یک شبکه عصبی به آن دست می یابیم ، حداقل سراسری تابع ما نیست، بلکه یک حداقل محلی و به اندازه کافی مناسب، برای انجام صحیح وظایفی است که ما در حال توسعه آن هستیم.

آنچه ما می خواهیم یک نرخ یادگیری مطلوب است که به ما امکان دهد که خطا را با گذشت زمان کاهش دهیم، تا زمانی که به حداقل خود برسیم. در نمودار، این نرخ یادگیری خط قرمز می باشد.

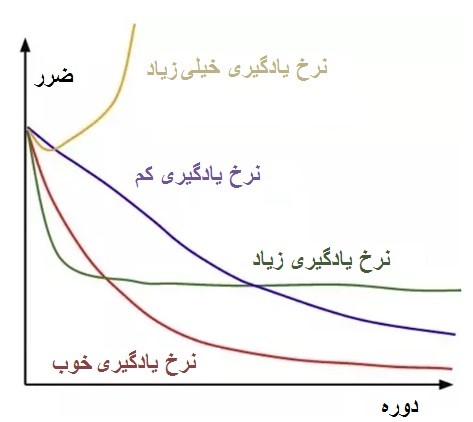
و برای رسیدن به حد مطلوب نرخ یادگیری، می توانیم یک تنزل به نرخ یادگیری خود اعمال کنیم. این تنزل نرخ یادگیری را با گذشت زمان کاهش می دهد، بنابراین هنگامی که به حداقل می رسیم به اندازه کافی کوچک خواهد بود که از پرش آن جلوگیری کنیم.

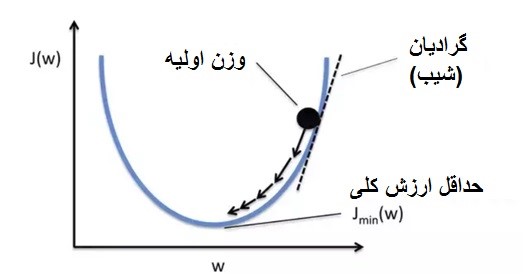
بنابراین،ما هم از انتظار طولانی برای همگرایی با انتخاب یک نرخ یادگیری بسیار کم، و هم پرش حداقل خود، جلوگیری می کنیم، زیرا هرچه به آن نزدیک تر باشیم، قدم هایی که در جهت رسیدن به آن بر می داریم، کوچکتر است.

اندازه دسته

برای یادآوری بخش قبلی، گرادیان نزولی تصادفی یک گرادیان نزولی تصادفی دسته کوچک است که در آن K = 1 قرار دارد.

و K در گرادیان نزولی تصادفی دسته کوچک ، تعداد نمونه های استفاده شده در هر بار به روز رسانی وزن ها را نشان می دهد. این یک پارامتر مهم نیست و معمولاً به حداکثر تعداد نمونه هایی که می توانند در GPU ما جای بگیرند، تعیین می شود.

ما یک GPU با ۸ گیگابایت حافظه داریم، اگر هر تصویر، ۱MB را اشغال کند، چند نمونه می توانیم از آن را جای بدهیم؟

خب، کار آسانی نیست! بستگی به معماری شبکه دارد. لایه های متراکم (  Dense) یا کاملاً متصل (Fully Connected  ) (که لایه های سنتی هستند که در آن همه نورون ها با همه نورون های موجود در لایه بعدی به هم پیوسته اند.) مواردی هستند که پارامترهای بیشتری دارند و بنابراین همان هایی هستند که حافظه بیشتری را اشغال می کنند.

ما همچنین لایه های کانولوشنی ، لایه های پولینگ، لایه های حذف کننده ( Dropout ) داریم. بنابراین در عمل، محاسبه حداکثر تعداد نمونه هایی که می توانیم استفاده کنیم، به صورت دستی دشوار است.

کاری که ما انجام می دهیم این است که اندازه های دسته ها را مضرب ۲ را تنظیم کرده و که در صورت خطای حافظه آن ها را کم کنیم. به عنوان مثال ، ما با ۵۱۲ شروع می کنیم و اگر خطایی داشته باشیم به ۲۵۶ ، ۱۲۸ ، ۶۴ ، ۳۲ ، ۱۶ ، ۸ ، ۴ ، ۲ و حتی ۱ پایین می رویم.

بسته به معماری شبکه شما، ممکن است مجبور شوید از K = 1 و به همین دلیل از گرادیان نزولی تصادفی استفاده کنید. اگرچه اغلب ترجیح داده می شود که اندازه تصویر را برای مثال مثال از   512در ۵۱۲ به ۲۵۶ در ۲۵۶ یا ۱۲۸ در ۱۲۸ پیکسل کاهش دهید و از یک K بزرگتر استفاده کنید.

ارتباط نرخ یادگیری و اندازه دسته

این نکته را باید در نظر داشته باشید که نرخ یادگیری به اندازه دسته مربوط است.

اگر به K = 1 نزدیک شویم، باید نرخ یادگیری را کم کنیم تا به روزرسانی های وزن ها اهمیت کمتری داشته باشند، زیرا به گرادیان نزولی تصادفی، به عبارت دیگر به محاسبات گرادیان با نمونه های تصادفی تک نزدیک تر است.

بنابراین، به طور خلاصه، اگر از یک اندازه دسته ی کمتری استفاده می کنیم، توصیه می شود از نرخ یادگیری کمتری استفاده شود اما ما باید تعداد دوره ها را نیز افزایش می دهیم، زیرا شرایط دوم باعث می شود که شبکه عصبی ما زمان بیشتری برای همگرایی صرف کند.

توابع ضرر و فعال سازی

تابع ضرر

تابع ضرر تابعی است که به ما می گوید پیش بینی های ما چقدر اشتباه بوده است.

تصور کنید که باید حدس بزنیم که فقط با دیدن یک عکس چقدر یک خانه می ارزید. شبکه عصبی ما پیکسل های عکس را به عنوان ورودی و عددی را به عنوان خروجی که قیمت را نشان می دهد، خواهد داشت.

به عنوان مثال، بیایید بگوییم که می خواهیم قیمت خانه را پیش بینی کنیم، بنابراین ما در حال آموزش شبکه هستیم و این خانه در مجموعه آموزشی ما است. هنگامی که تصویر عبور می کند، یک پیش بینی محاسبه می شود، که یعنی ارزش آن ۳۲۳،۵۶۷ دلار است. حقیقت این است که خانه ۶۰۰۰۰۰ دلار ارزش دارد، بنابراین به طور واضح به نظر می رسد که یک تابع ضرر مناسب می تواند به صورت زیر باشد:

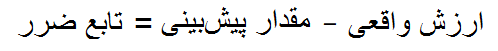
با در نظر گرفتن این نکته، متداول ترین توابع ضرر عبارتند از:

برای مسائل رگرسیون

• میانگین مربعات خطا (Mean Squared Error )
• میانگین خطای مطلق ( Mean Absolute Error )

برای مسائل طبقه بندی

• اختلاف آنتروپی دو دویی ( Binary Cross-Entropy )
• اختلاف آنتروپی موضوعی ( Categorical Cross-Entropy )

بیایید نگاهی به هر یک از آن ها بیندازیم:

• میانگین مربعات خطا :

میانگین مربعات خطا یا  MSE، میانگین اختلاف مربعات بین نقاط داده واقعی و نتیجه پیش بینی شده است. در این روش هرچه فاصله بزرگتر باشد، آن را بیشتر جریمه می کند که روش  استاندارد در مسائل رگرسیون است.

• میانگین خطای مطلق :

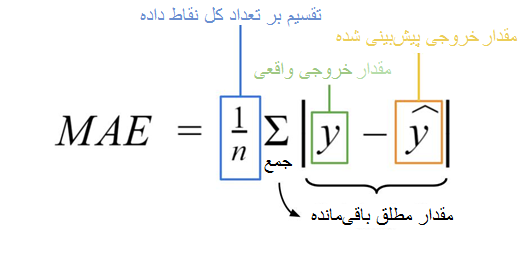
خطا میانگین مطلق یا  MAE، میانگین اختلاف مطلق بین نقاط داده واقعی و نتیجه پیش بینی شده است. اگر ما این روش را به عنوان استراتژی برای پیش برد کار در نظر بگیریم، هر مرحله از “گرادیان نزولی” باعث کاهش MAE می شود.

اختلاف آنتروپی چیست؟

ابتدا باید بدانیم که آنتروپی چیست. پس بیایید این موضوع را با چند مثال نشان دهیم:

مثال ۱

تصور کنید که ما در حال انجام یک بازی هستیم: یک کیسه با توپ های رنگی مختلف داریم و هدف بازی این است که با تعداد حداقل سوالات، حدس بزنید که داوطلب کدام یک از رنگ ها را بیرون کشیده است.

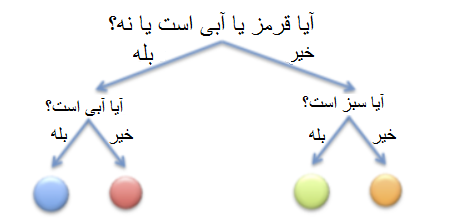
در این مورد، ما یک توپ آبی، یک توپ قرمز، یک توپ سبز و یک توپ نارنجی داریم:

این به این معنی است که هر توپ احتمال خروج ۴/۱ را دارد.

یکی از بهترین راهکار ها این است که ابتدا سؤال کنید که آیا توپی که شما ارائه داده اید آبی یا قرمز است یا نه. اگر چنین باشد، می پرسیم توپ آبی است یا خیر، اگر اینگونه نباشد، می پرسیم سبز است یا خیر. بنابراین ما به ۲ سؤال نیاز داریم.

مثال ۲

این بار کیسه ای از توپ هایی داریم که در آن ۲/۱ آبی، ۴/۱ قرمز، ۸/۱ با رنگ سبز و ۸/۱ نارنجی است. اکنون، استراتژی بهینه این است که ابتدا بپرسید که آیا آبی رنگ است یا خیر زیرا احتمال بهتری برای بیرون آمدن آبی وجود دارد. اگر چنین باشد، بازی ما تمام است. اگر اینطور نیست، می توانیم بپرسیم که آیا قرمز است یا خیر، که کلاس بعدی در احتمال است. اگر چنین باشد ، بازی ما تمام شده است. اگر نه، می توانیم بپرسیم که آیا آن سبز است یا خیر (یا آیا نارنجی است یا خیر).

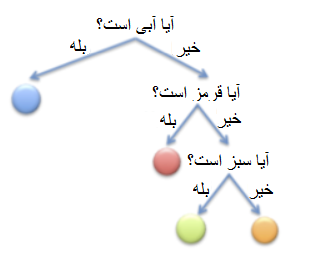
حال اتفاقی که می افتد این است که نیمی از مواقع (۲/۱) آبی است و برای حدس زدن ما ۱ سوال هزینه می شود.۴/۱ مواقع قرمز است و ۲ سوال برای ما هزینه دارد. ۸/۱ سبز است و ۳ سوال برای ما هزینه دارد و اگر نارنجی باشد نیز همین است.

بنابراین، تعداد سؤالات مورد انتظار برای حدس زدن یک توپ عبارتند از:

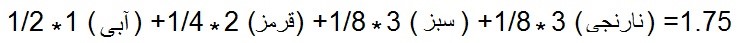
مثال ۳

اکنون تصور کنید که یک کیسه پر از توپ های آبی داریم. چند سؤال نیاز داریم که بفهمیم رنگ توپی که آن ها بیرون می کشند، چیست؟ هیچ، ۰

از این مثال ها می توانیم عبارتی را بیابیم که به ما امکان می دهد بسته به احتمال توپ تعداد سؤالات را محاسبه کنیم. بنابراین ، یک توپ با احتمال p سؤال های log₂ ^(1/p) را نیاز دارد.

به عنوان مثال، برای توپ که دارای p = 1/8 است ، ما نیاز داریم به تعداد سوالات:

n_quest=log2(1/(1/8)=3

بنابراین تعداد سؤالات مورد انتظار در کل برابر است با:

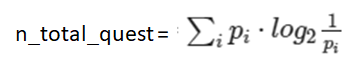
در پایان، یک راه برای درک آنتروپی به شرح زیر است:

اگر ما دنبال استراتژی بهینه بودیم، تعداد سوالات مورد انتظار که به ما اجازه می دهد رنگ توپ را حدس بزنیم، چند تا است؟

بنابراین ، هرچه بازی پیچیده تر باشد، آنتروپی بالاتر است. در این حالت، مثال ۱> مثال ۲> مثال ۳٫

خب، بنابراین اکنون که ما می دانیم آنتروپی چیست، بیایید ببینیم اختلاف آنتروپی چیست.

اختلاف آنتروپی:

تصور کنید که استراتژی مثال ۱ را برای مثال ۲ پیش گرفته ایم:

بنابراین، ما باید دو سؤال می پرسیدیم تا دریابیم که رنگ آن هر چه که بوده است. اگر تعداد کل سؤالات مورد نیاز را محاسبه کنیم، با به حساب آوردن اینکه این بار هر توپ یک احتمال دارد، داریم:

بنابراین این استراتژی از استراتژی استفاده شده در مثال ۱ بدتر است.

در پایان ، منطقا، آنتروپی تعداد سؤالات مورد انتظار با استفاده از بهترین استراتژی ممکن است و اختلاف آنتروپی تعداد سوالات مورد انتظار در هنگام استفاده نکردن از بهترین استراتژی می باشد.

به همین دلیل ، کاری که ما سعی می کنیم انجام دهیم حداقل سازی اختلاف آنتروپی است.

به طور رسمی ، اینگونه تعریف می شود:

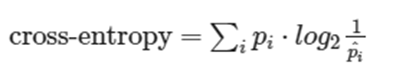
که در آن:

• pi احتمال واقعی توپ ها است. (در مثال ما ۱/۲ برای آبی ، ۱/۴ برای قرمز و ۱/۸ برای سبز و نارنجی)
• pi^ احتمالی است که هنگام استفاده از استراتژی خود فرض کرده ایم، که در این حالت این است که همه توپ ها به همان اندازه محتمل هستند. (۱/۴ برای همه رنگ ها)

یک راه برای به یاد آوردن این که چه چیزی در کجای فرمول قرار دارد، این است که بخاطر بسپاریم آنچه می خواهیم انجام دهیم این است که دریابیم چند سؤال در طی استراتژی ما، که pi^ است، لازم است، بنابراین در داخل log2، pi^ قرار می گیرد.

توابع فعالسازی

اگر ما توابع فعال سازی نداشتیم، شبکه ی ما به صورت زیر می شد:

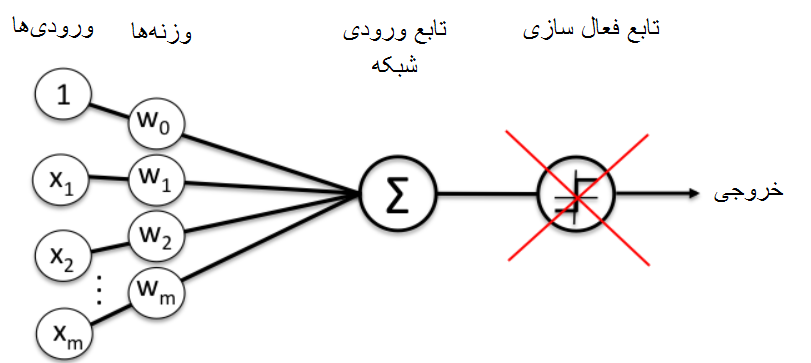
ما مجبور به استفاده از y (x) = Wx + b بودیم. این یک ترکیب خطی است که حتی قادر به حل مشکلی مانند XOR هم نیست.

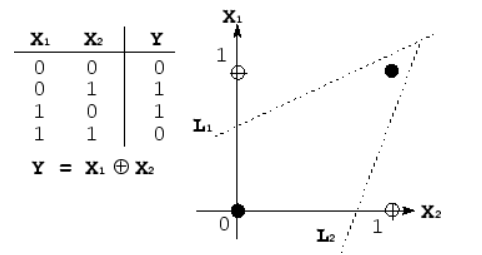
بنابراین، ما به راهی برای معرفی غیرخطی نیاز داریم و این همان کاری است که تابع فعال سازی انجام می دهد. در تصویر زیر می توانید برخی از نمونه های رایج را مشاهده کنید، و جایی که آن ها در شبکه مداخله می کنند:

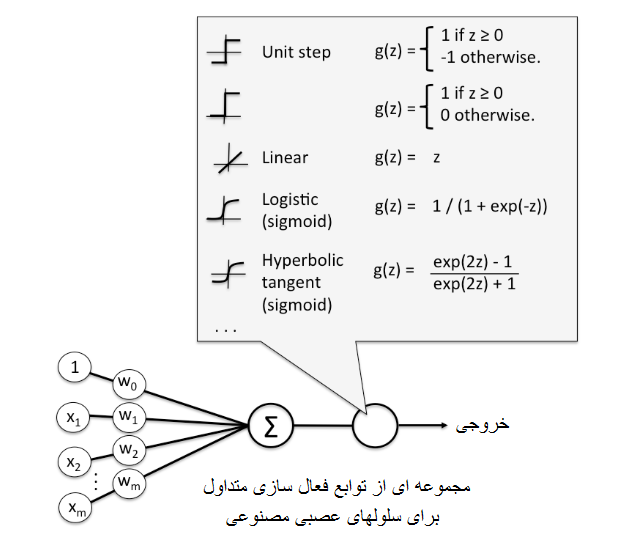
در اینجا می توانید بیشترین موارد استفاده شده را مشاهده کنید:

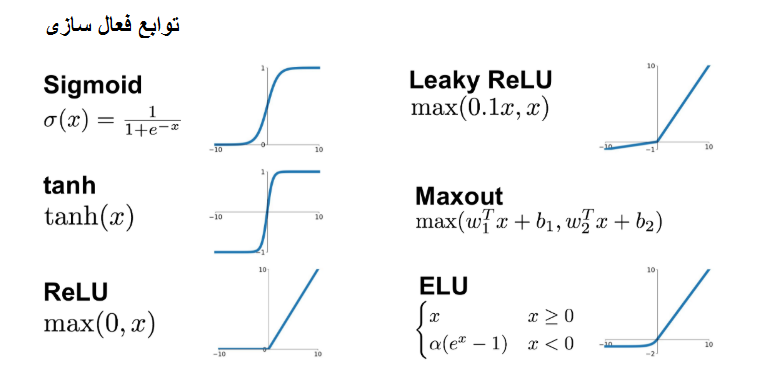
سخت است بدانید که شبکه ما با کدام یک رفتار بهتری خواهد داشت، اما معمولاً یکی وجود دارد که تقریباً همیشه نتایج خوبی می دهد: تابع  ReLU.

بنابراین، هر زمان که شروع کنیم، از تابع ReLU استفاده خواهیم کرد و به محض اینکه نتیجه ای بدست آوردیم که آن را خوب می دانیم، می توانیم با تابع Leaky ReLU یا هر مورد دیگری که می خواهید، امتحان کنیم. هر روز موارد جدیدی بیرون می آیند، و یک جستجوی ساده گوگل می تواند شما را به موارد جالبی سوق دهد: مثلاً SELU

بسیاری از این توابع فعال سازی نیاز به روش های مشخصی از وزن دهی اولیه دارند تا بین یک محدوده خاص از مقادیر قرار بگیرند که گرادیان نزولی به درستی کار می کند.

در مورد لایه های خروجی، تابع فعال سازی softmax یکی از بیشترین موارد مصرف است، زیرا این قابلیت را دارد که به هر کلاس احتمال بدهد، و باعث می شود که احتمال همه آن ها را تا ۱ بالا ببرد.

از آنجا که این ممکن است کمی پیچیده به نظر برسد، ادامه دستورالعمل توصیه شده به عنوان خلاصه ای از موارد ذکر شده در بالا گفته شده است:

دستورالعمل:

• استفاده از ReLU را با نرخ یادگیری ۰٫۰۱ یا ۰٫۰۰۱ شروع کنید و ببینید که چه اتفاقی می افتد.
• اگر شبکه آموزش می یابد ( همگرا می شود ) اما کند است، می توانید کمی نرخ یادگیری را افزایش دهید.
• اگر شبکه همگرا نمی شود و نامنظم رفتار می کند، نرخ یادگیری را کاهش دهید.
• هنگامی که شما شبکه خود را درحال اجرا دیدیدLeaky ReLU ، Maxout یا ELU را امتحان کنید.
• از sigmoid استفاده نکنید، در عمل معمولاً نتایج خوبی نمی دهد.

مقدار دهی اولیه وزن

همانطور که قبلاً مشاهده کرده اید، مقداردهی اولیه وزن ها و بایاس برای دستیابی به همگرایی شبکه ما به یک حداقل مقدار کافی، بسیار مهم است. بنابراین بیایید به برخی از روش ها برای مقداردهی اولیه وزن ها توجه کنیم.

اگر از مجموعه داده MNIST استفاده می کنیم ماتریس وزن ما  768 ( ورودی ) در ۱۰ ( خروجی ) خواهد بود.

مقدار دهی اولیه ثابت

ما می توانیم وزن خود را از قبل تنظیم کنیم به:

صفر:

W = np.zeros((768, 10))

یک:

W = np.ones((768, 10))

یک مقدار ثابت C :

W = np.ones((768, 10)) * C

توزیع نرمال و یکنواخت

ما همچنین می توانیم وزن ها را با استفاده از توزیع یکنواخت مقدار اولیه بدهیم، جایی که یک [ upper_bound،Lower_bound ] تعریف شده است و تمام اعداد در محدوده، احتمال انتخاب یکسان دارند.

برای مثال، برای یک توزیع بین [-۰٫۲،۰٫۲] [- ۰٫۲،۰٫۲] داریم:

W = np.random.uniform(low=-0.2, high=0.2, size=(768, 10))

با این دستورالعمل، ما ماتریس وزنی WW را با مقادیر استخراج شده از محدوده بین [-۰٫۲،۰٫۲] [- ۰٫۲٫۰٫۲] که در آن همه ی آن ها احتمال استخراج یکسان دارند، آغاز می کنیم.

ما همچنین می توانیم این کار را با یک توزیع عادی یا گوسی انجام دهیم، که به صورت زیر تعریف شده است:

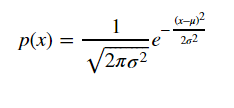
که همانطور که می دانید:

• μ میانگین است.
• σ انحراف استاندارد و σ^۲ واریانس است.

بنابراین می توانیم وزن خود را با توزیع نرمال با μ = ۰ و σ = ۰٫۲ مقدار اولیه بدهیم، به عنوان مثال:

W = np.random.normal(0.0, 0.2, size=(768, 10))

مقدار دهی اولیه : LeCun نرمال و یکنواخت

روش پیشرفته تر دیگر، روش LeCun است که به عنوان پس انتشار کارآمد نیز شناخته می شود.

این روش ۳ پارامتر را تعریف می کند:

• Fin: تعداد ورودی های لایه (در مثال ما ۷۶۸)
• Fout: تعداد خروجی های لایه (در مثال ما ۱۰)
• Limit(حد): مطابق با Fin و Fout به صورت زیر تعریف می شود:

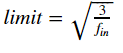
کد مورد نیاز برای مقدار دهی اولیه W با این روش با استفاده از توزیع یکنواخت به صورت زیر می باشد:

W = np.random.uniform(low=-limit, high=limit, size=(F_in, F_out))

و برای یک توزیع نرمال داریم:

W = np.random.normal(low=-limit, high=limit, size=(F_in, F_out))

مقدار دهی اولیه: Glorot / Xavier نرمال و یکنواخت

این شاید متداول ترین روش برای مقدار دهی اولیه وزن ها و بایاس باشد. هنگام استفاده از Keras پیش فرض است.

در این حالت ، پارامترهای مشابه با LeCun نیز تعریف می شوند، اما محاسبه limit متفاوت است:

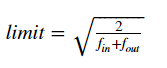
کد مقدار دهی اولیه WW با استفاده از این روش می تواند همانند LeCun باشد.

برای توزیع یکنواخت به صورت زیر خواهد بود:

W = np.random.uniform(low=-limit, high=limit, size=(F_in, F_out))

و برای توزیع نرمال داریم:

W = np.random.normal(low=-limit, high=limit, size=(F_in, F_out))

مقدار دهی اولیه: هی (He) و همکاران/Kaiming/MSRA نرمال و یکنواخت

این روش به نام Kaiming He، اولین نویسنده ” کاوش عمیق در اصلاح کننده ها : برتری از سطح انسانی در طبقه بندی ImageNet ” نامگذاری شده است.

به طور معمول، این روش زمانی مورد استفاده قرار می گیرد که ما شبکه های عصبی بسیار عمیقی را آموزش می دهیم که از نوع خاصی از ReLU به عنوان فعال سازی مانند ReLU پارامتری استفاده می شود.

کد در این مورد توزیع یکنواخت به صورت زیر است:

limit = np.sqrt(6 / float(F_ini))
W = np.random.uniform(low=-limit, high=limit, size=(F_in, F_out))

و در مورد توزیع نرمال اینگونه است:

limit = np.sqrt(2 / float(F_ini))
W = np.random.uniform(low=-limit, high=limit, size=(F_in, F_out))

دستورالعمل:

مقدار دهی اولیه وزن ها معمولاً عاملی تعیین کننده در آموزش یک شبکه نیست، اما گاهی اوقات می تواند باعث شود که شبکه قادر به آموزش نباشد، زیرا در همگرایی ناکام است.

بنابراین، توصیه می شود که از Glorot استفاده کنید، و اگر آن روز احساس خوش شانسی کردید و می خواهید ببینید که آیا می توانید در دقت پیشرفت کنید، با دیگر توابع امتحان کنید.

سخن پایانی :

مثل همیشه، امیدوارم که شما از این پست لذت برده باشید، که اکنون در شبکه های عصبی حرفه ای هستید!

اگر این پست را دوست داشتید، می توانید به پست های دیگر ما در زمینه ی یادگیری ماشین نگاهی بیندازید.

بیشتر بخوانید :

• گوگل ساختار سازمانی خود را جهت تمرکز بر هوش مصنوعی اصلاح می کند
• پلاک خوان های شهر گرینزبوروی آمریکا فعلاً قرار نیست افزایش پیدا کنند
• فرماندار اوکلند از پلاک خوان ها حمایت می کند اما مخالفان در اثربخشی آن تردید دارند
• لبنان استفاده از پلاک خوان های خودکار را تایید کرد
• چالش های مدیریت کلاس با ابزار جدید تشخیص چهره هوش مصنوعی

منبع Towards Data Science